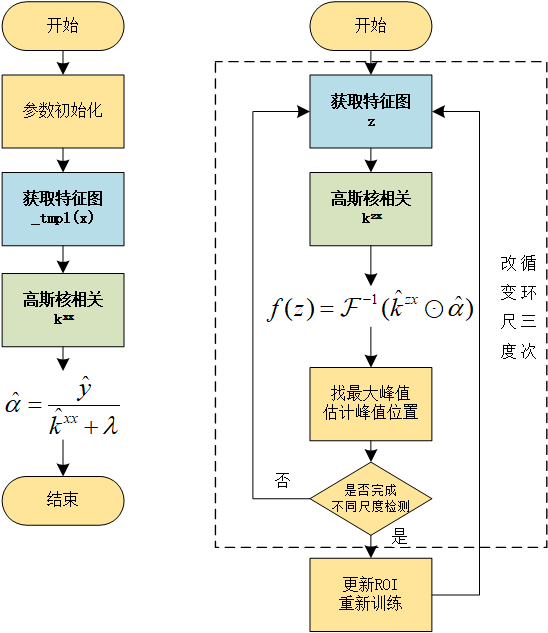
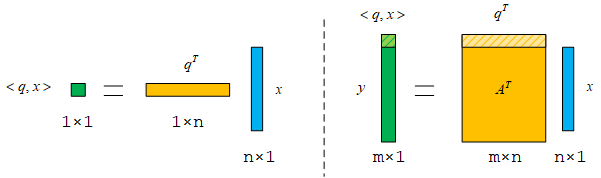从2015年João F. Henriques等人提出KCF以来,网上已经有了很多相关的科普,也有博主给出了非常详细的推导 ,但如果想要真正理解我觉得还是得自己推导一遍,所以我在这里准备写一下自己学习过程中的一些想法。推导有问题 ,我推导了之后也发现确实是有那个问题,但无伤大雅。
上面的这些链接是我的主要参考资料。
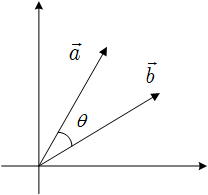
向量内积
在二维平面中,两个向量如果长度相同,它们之间的相似程度可以用它们之间的夹角来衡量。c o s ( θ ) cos(\theta) cos ( θ ) a ⃗ \vec a a b ⃗ \vec b b ( x 1 , y 1 ) (x_1, y_1) ( x 1 , y 1 ) ( x 2 , y 2 ) (x_2, y_2) ( x 2 , y 2 )
c o s ( θ ) = a ⃗ ⋅ b ⃗ ∣ a ⃗ ∣ ∣ b ⃗ ∣ = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 x 2 2 + y 2 2 cos(\theta)=\frac{\vec a\cdot \vec b}{|\vec a||\vec b|}=\frac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2} }
cos ( θ ) = ∣ a ∣∣ b ∣ a ⋅ b = x 1 2 + y 1 2 x 2 2 + y 2 2 x 1 x 2 + y 1 y 2
前一个等号是通过余弦定理得到的。
∣ a ⃗ − b ⃗ ∣ 2 = ∣ a ⃗ ∣ 2 + ∣ b ⃗ ∣ 2 − 2 ∣ a ⃗ ∣ ∣ b ⃗ ∣ c o s ( θ ) |\vec a - \vec b|^2 = |\vec a|^2+|\vec b|^2-2|\vec a||\vec b|cos(\theta)
∣ a − b ∣ 2 = ∣ a ∣ 2 + ∣ b ∣ 2 − 2∣ a ∣∣ b ∣ cos ( θ )
化简上面这个式子就可以得到结论。那么为什么两个向量相乘是对应的坐标相乘呢?因为两个向量的坐标是在一组正交基为基底表示的。a ⃗ = x 1 e 1 + y 1 e 2 \vec a = x_1e_1+y_1e_2 a = x 1 e 1 + y 1 e 2 e 1 , e 2 e_1,e_2 e 1 , e 2
a ⃗ ⋅ b ⃗ = ( x 1 e 1 + y 1 e 2 ) ( x 2 e 1 + y 2 e 2 ) = x 1 x 2 + y 1 y 2 \vec a \cdot \vec b=(x_1e_1+y_1e_2)(x_2e_1+y_2e_2)=x_1x_2+y_1y_2
a ⋅ b = ( x 1 e 1 + y 1 e 2 ) ( x 2 e 1 + y 2 e 2 ) = x 1 x 2 + y 1 y 2
从上面的例子中可以看到,向量内积在两个向量的长度相同的前提下能够反映两个向量的夹角大小 。
向量范数
向量范数被用来衡量向量的长度。严格的数学定义我就不写了,我感觉只要能够知道L-p范数的形式就行,L-p范数用∣ ∣ ⋅ ∣ ∣ p ||\cdot||_p ∣∣ ⋅ ∣ ∣ p
∣ ∣ ⋅ ∣ ∣ p : = ( ∑ i = 1 i = n x i p ) 1 p ||\cdot||_p:=\left(\sum\limits_{i = 1}^{i = n} x_i^p\right)^{\frac{1}{p} }
∣∣ ⋅ ∣ ∣ p := ( i = 1 ∑ i = n x i p ) p 1
L 2 L^2 L 2 L 2 L^2 L 2 ∣ ∣ ⋅ ∣ ∣ 2 ||\cdot||_2 ∣∣ ⋅ ∣ ∣ 2 ∣ ∣ ⋅ ∣ ∣ 2 ||\cdot||^2 ∣∣ ⋅ ∣ ∣ 2
Gram矩阵与协方差矩阵
Gram矩阵和协方差矩阵都可以用X H X X^HX X H X X X H XX^H X X H X H X X^HX X H X X X H XX^H X X H
计算得到的方阵中,对角线上元素是每个样本向量自己和自己内积的结果;非对角线元素是不同样本向量之间的内积。
DFT与DFT的矩阵表示
DFT的本质还是DFS,我觉得DFT只是DFS的一种表示方式。我们处理的序列是有限长的,可以把时域上的序列周期延拓,那样就可以用DFS处理。DFS的主值区间的系数就是DFT的结果。所以在做DFT分析的时候一定要注意序列隐含的周期性 。
x ^ [ k ] = ∑ n = 0 N − 1 x [ n ] W N k n \hat x[k]=\sum \limits_{n=0}^{N-1}x[n]W_N^{kn}
x ^ [ k ] = n = 0 ∑ N − 1 x [ n ] W N kn
DFT合成式(IDFT):
x [ n ] = 1 N ∑ k = 0 N − 1 x ^ [ k ] W N − k n x[n]=\frac{1}{N}\sum \limits_{k=0}^{N-1}\hat x[k]W_N^{-kn}
x [ n ] = N 1 k = 0 ∑ N − 1 x ^ [ k ] W N − kn
上面的式子中x ^ [ k ] \hat x[k] x ^ [ k ] x [ n ] x[n] x [ n ] W N k n W_N^{kn} W N kn W N = e − j 2 π / N W_N=e^{-j2\pi/N} W N = e − j 2 π / N W N W_N W N
x ^ [ k ] = [ 1 1 1 1 ⋯ 1 1 W N 1 W N 2 W N 3 ⋯ W N N − 1 1 W N 2 W N 4 W N 6 ⋯ W N 2 ( N − 1 ) 1 W N 3 W N 6 W N 9 ⋯ W N 3 ( N − 1 ) ⋮ ⋮ ⋮ ⋮ ⋱ ⋮ 1 W N N − 1 W N 2 ( N − 1 ) W N 3 ( N − 1 ) ⋯ W N ( N − 1 ) ( N − 1 ) ] [ x [ 0 ] x [ 1 ] x [ 2 ] x [ 3 ] ⋮ x [ N − 1 ] ] = F x [ n ] \hat x[k]= {\begin{bmatrix}
1&1&1&1& \cdots &1\\
1&W_N^1&W_N^2&W_N^3& \cdots &W_N^{N-1}\\
1&W_N^2&W_N^4&W_N^6& \cdots &W_N^{2(N-1)}\\
1&W_N^3&W_N^6&W_N^9& \cdots &W_N^{3(N-1)}\\
\vdots & \vdots & \vdots & \vdots& \ddots & \vdots \\
1&W_N^{N-1}&W_N^{2(N-1)}&W_N^{3(N-1)}& \cdots &W_N^{(N-1)(N-1)}
\end{bmatrix} } {\begin{bmatrix}
x[0]\\
x[1]\\
x[2]\\
x[3]\\
\vdots\\
x[N-1]
\end{bmatrix} } = Fx[n] x ^ [ k ] = ⎣ ⎡ 1 1 1 1 ⋮ 1 1 W N 1 W N 2 W N 3 ⋮ W N N − 1 1 W N 2 W N 4 W N 6 ⋮ W N 2 ( N − 1 ) 1 W N 3 W N 6 W N 9 ⋮ W N 3 ( N − 1 ) ⋯ ⋯ ⋯ ⋯ ⋱ ⋯ 1 W N N − 1 W N 2 ( N − 1 ) W N 3 ( N − 1 ) ⋮ W N ( N − 1 ) ( N − 1 ) ⎦ ⎤ ⎣ ⎡ x [ 0 ] x [ 1 ] x [ 2 ] x [ 3 ] ⋮ x [ N − 1 ] ⎦ ⎤ = F x [ n ]
F F F F F F x [ n ] x[n] x [ n ] x ^ [ k ] \hat x[k] x ^ [ k ] x ^ [ k ] \hat x[k] x ^ [ k ] x [ n ] x[n] x [ n ]
DFT矩阵的性质
DFT矩阵F F F F T = F F^T=F F T = F F H = F ∗ F^H=F^* F H = F ∗
F F H = [ s 0 0 ⋯ 0 0 s 0 ⋯ 0 0 0 s ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ s ] = s I s FF^H={\begin{bmatrix}
s&0&0& \cdots &0\\
0& s& 0 & \cdots &0\\
0 & 0& s& \cdots & 0\\
\vdots & \vdots& \vdots& \ddots& \vdots\\
0& 0& 0& \cdots& s\\
\end{bmatrix} }=s\boldsymbol I_s F F H = ⎣ ⎡ s 0 0 ⋮ 0 0 s 0 ⋮ 0 0 0 s ⋮ 0 ⋯ ⋯ ⋯ ⋱ ⋯ 0 0 0 ⋮ s ⎦ ⎤ = s I s
前面分析的时候,x [ n ] x[n] x [ n ] x ^ [ k ] \hat x[k] x ^ [ k ] s s s F − 1 F^{-1} F − 1
F − 1 = 1 s F H F^{-1}=\frac{1}{s}F^H
F − 1 = s 1 F H
F − 1 F^{-1} F − 1 x [ n ] = F − 1 F x [ n ] x[n]=F^{-1}Fx[n] x [ n ] = F − 1 F x [ n ]
酉矩阵(Unitary Matrix)
F F F U U H = U H U = I UU^H=U^HU=I U U H = U H U = I
( 1 s F ) ( 1 s F H ) = I s {\left (\frac{1}{\sqrt s}F\right )}\left( \frac{1}{\sqrt s}F^H\right )=I_s
( s 1 F ) ( s 1 F H ) = I s
所以1 s F \frac{1}{\sqrt s}F s 1 F L 2 L^2 L 2 U = 1 s F U=\frac{1}{\sqrt s}F U = s 1 F F F F U U U U H = U ∗ U^H=U^* U H = U ∗ U U U 1 s F \frac{1}{\sqrt s}F s 1 F
{ ∣ ∣ x ∣ ∣ 2 = x H x ∣ ∣ U x ∣ ∣ 2 = x H U H U x = x H x \left \{
\begin {matrix}
||x||^2=x^Hx\\
||Ux||^2=x^HU^HUx=x^Hx
\end {matrix}
\right . { ∣∣ x ∣ ∣ 2 = x H x ∣∣ Ux ∣ ∣ 2 = x H U H Ux = x H x
这是酉矩阵都具有的性质,除此之外还可以根据这一关系推导出帕斯瓦尔定理,信号在时频域的能量相等。
∣ ∣ x ∣ ∣ 2 = ∣ ∣ U x ∣ ∣ 2 = ∣ ∣ 1 s F x ∣ ∣ 2 = 1 s ∣ ∣ x ^ ∣ ∣ 2 ||x||^2=||Ux||^2=||\frac{1}{\sqrt s}Fx||^2=\frac{1}{s}||\hat x||^2
∣∣ x ∣ ∣ 2 = ∣∣ Ux ∣ ∣ 2 = ∣∣ s 1 F x ∣ ∣ 2 = s 1 ∣∣ x ^ ∣ ∣ 2
循环卷积
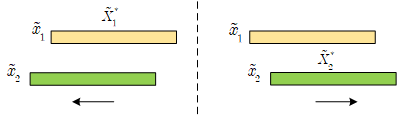
频域乘积等于时域卷积。DFT也有这一性质,考虑到DFT隐含的周期性,循环卷积需要从DFS的周期卷积开始讲起。s s s x ~ 1 [ n ] \tilde x_1[n] x ~ 1 [ n ] x ~ 2 [ n ] \tilde x_2[n] x ~ 2 [ n ] s s s X ~ 1 [ k ] \tilde X_1[k] X ~ 1 [ k ] X ~ 2 [ k ] \tilde X_2[k] X ~ 2 [ k ] x ~ 1 [ n ] \tilde x_1[n] x ~ 1 [ n ] x ~ 2 [ n ] \tilde x_2[n] x ~ 2 [ n ]
x ~ 3 [ n ] = ∑ m = 0 s − 1 x ~ 1 [ m ] x ~ 2 [ n − m ] \tilde x_3[n]=\sum\limits_{m = 0}^{s - 1} { { {\tilde x}_1}[m]{ {\tilde x}_2}[n - m]}
x ~ 3 [ n ] = m = 0 ∑ s − 1 x ~ 1 [ m ] x ~ 2 [ n − m ]
X ~ 3 [ k ] {\tilde X_3}[k] X ~ 3 [ k ] x ~ 3 \tilde x_3 x ~ 3
X ~ 3 [ k ] = ∑ n = 0 s − 1 ( ∑ m = 0 s − 1 x ~ 1 [ m ] x ~ 2 [ n − m ] ) W N k n = ∑ m = 0 s − 1 x ~ 1 [ m ] ∑ n = 0 s − 1 x ~ 2 [ n − m ] W N k ( n − m ) W N k m {\tilde X_3}[k] = \sum \limits_{n = 0}^{s - 1} \left( {\sum\limits_{m = 0}^{s - 1} { { {\tilde x}_1}[m]{ {\tilde x}_2}[n - m]} } \right)W_N^{kn} = \sum\limits_{m = 0}^{s - 1} { { {\tilde x}_1}[m]\sum\limits_{n = 0}^{s - 1} { { {\tilde x}_2}[n - m]W_N^{k(n - m)}W_N^{km} } }
X ~ 3 [ k ] = n = 0 ∑ s − 1 ( m = 0 ∑ s − 1 x ~ 1 [ m ] x ~ 2 [ n − m ] ) W N kn = m = 0 ∑ s − 1 x ~ 1 [ m ] n = 0 ∑ s − 1 x ~ 2 [ n − m ] W N k ( n − m ) W N km
= ∑ m = 0 s − 1 x ~ 1 [ m ] W N k m X ~ 2 [ k ] = X ~ 1 [ k ] X ~ 2 [ k ] = \sum\limits_{m = 0}^{s - 1} { { {\tilde x}_1}[m]W_N^{km} } { {\tilde X}_2}[k] = { {\tilde X}_1}[k]{ {\tilde X}_2}[k]
= m = 0 ∑ s − 1 x ~ 1 [ m ] W N km X ~ 2 [ k ] = X ~ 1 [ k ] X ~ 2 [ k ]
先周期卷积再计算DFS可以通过交换求和顺序,来推导出时域卷积等于频域乘积的结论。回到DFT上,循环卷积实际上和周期卷积是同样的数值计算,只是换一种说法而已。只有循环卷积才能用DFT来加速运算 ,如果是做线性卷积,那么需要对循环卷积的长度做调整,然后才能用DFT,因为循环卷积相当于是一种有混叠的线性卷积。不过好在论文里要用的都是循环卷积,所以可以直接用DFT加速。
相关运算
自相关和互相关都是相关运算。自相关(auto-correlation)和互相关(cross-correlation)顾名思义就是序列自身和自身做相关运算,或者是两个序列之间做相关运算。
x ~ 3 [ n ] = ∑ m = 0 s − 1 x ~ 1 [ m ] x ~ 2 [ n + m ] \tilde x_3[n]=\sum \limits_{m=0}^{s-1}\tilde x_1[m]\tilde x_2[n+m]
x ~ 3 [ n ] = m = 0 ∑ s − 1 x ~ 1 [ m ] x ~ 2 [ n + m ]
上面的式子就表示x ~ 1 \tilde x_1 x ~ 1 x ~ 2 \tilde x_2 x ~ 2 x ~ 1 \tilde x_1 x ~ 1
X ~ 3 [ k ] = ∑ n = 0 s − 1 ( ∑ m = 0 s − 1 x ~ 1 [ m ] x ~ 2 [ n + m ] ) W N k n = ∑ m = 0 s − 1 x ~ 1 [ m ] ∑ n = 0 s − 1 x ~ 2 [ n + m ] W N k ( n + m ) W N − k m {\tilde X_3}[k] = \sum \limits_{n = 0}^{s - 1} \left( {\sum\limits_{m = 0}^{s - 1} { { {\tilde x}_1}[m]{ {\tilde x}_2}[n+m]} } \right)W_N^{kn} = \sum\limits_{m = 0}^{s - 1} { { {\tilde x}_1}[m]\sum\limits_{n = 0}^{s - 1} { { {\tilde x}_2}[n+ m]W_N^{k(n + m)}W_N^{-km} } }
X ~ 3 [ k ] = n = 0 ∑ s − 1 ( m = 0 ∑ s − 1 x ~ 1 [ m ] x ~ 2 [ n + m ] ) W N kn = m = 0 ∑ s − 1 x ~ 1 [ m ] n = 0 ∑ s − 1 x ~ 2 [ n + m ] W N k ( n + m ) W N − km
= ∑ m = 0 s − 1 x ~ 1 [ m ] W N − k m X ~ 2 [ k ] = X ~ 1 ∗ [ k ] X ~ 2 [ k ] = \sum\limits_{m = 0}^{s - 1} { { {\tilde x}_1}[m]W_N^{-km} } { {\tilde X}_2}[k] = {\tilde X_1^*}[k]{ {\tilde X}_2}[k]
= m = 0 ∑ s − 1 x ~ 1 [ m ] W N − km X ~ 2 [ k ] = X ~ 1 ∗ [ k ] X ~ 2 [ k ]
相关运算结果的傅里叶级数是也是两个序列的傅里叶级数相乘,只不过其中一个傅里叶级数需要求复共轭。X ~ 3 [ k ] {\tilde X_3}[k] X ~ 3 [ k ]
X ~ 3 [ k ] = D F S ( x ~ 1 [ n ] ) D F S ( x ~ 2 [ − n ] ) = X ~ 1 [ k ] X ~ 2 ∗ [ k ] \tilde X_3[k]=DFS(\tilde x_1[n])DFS(\tilde x_2[-n])=\tilde X_1[k]\tilde X_2^*[k]
X ~ 3 [ k ] = D FS ( x ~ 1 [ n ]) D FS ( x ~ 2 [ − n ]) = X ~ 1 [ k ] X ~ 2 ∗ [ k ]
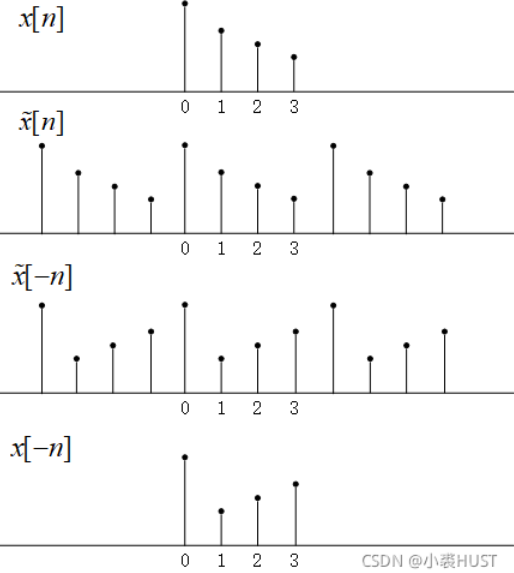
这时候就有问题了?到底是哪个序列需要求复共轭?经过观察可以发现,一个序列在另一个序列上滑动是有两种情况的,不同的情况对应着不同的求复共轭的情况。
当x ~ 2 \tilde x_2 x ~ 2 x ~ 1 \tilde x_1 x ~ 1 X ~ 1 \tilde X_1 X ~ 1 x ~ 1 \tilde x_1 x ~ 1 x ~ 2 \tilde x_2 x ~ 2 X ~ 2 \tilde X_2 X ~ 2