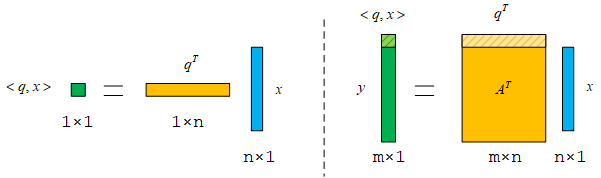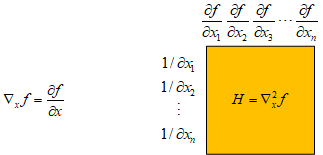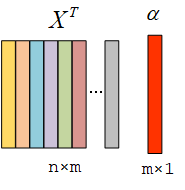CSK与KCF算法推导（二）

本文是CSK与KCF算法推导的第二篇，主要介绍标量对向量求导、核函数、岭回归问题求解等内容。

向量求导

很多论文里的数学推导都离不开对向量求导。对向量求导的本质也是对一个个分量求导，用向量写起来就非常紧凑美观。向量分为行向量和列向量，习惯上我们都是把变量写成列向量，所以大多数情况都是对列向量求导。有些书里提出了“分子布局”、“分母布局”的概念，帮助阐述如何对向量求导，但我怕比较繁琐就不在这里介绍了。

标量对向量求导

两个向量的内积可以得到一个标量，这个标量对向量求导实际上是对向量的每个分量分别求导。设 $q=\{q_1, q_2,q_3\cdots q_n\}^T$ ， $x=\{x_1,x_2,x_3,\cdots x_n\}^T$ ， $q$ 和 $x$ 都是n维的列向量。把 $q$ 和 $x$ 的内积写成多项式的形式：

$y=<q,x>=q^Tx=x^Tq=q_1x_1+q_2x_2+q_3x_3+\cdots+q_nx_n$

然后分别对 $x$ 的每个分量求导，结果也可以写成列向量。

$\frac {\partial y}{\partial x}=\frac {\partial q^Tx}{\partial x}=\frac {\partial x^Tq}{\partial x}= {\begin {bmatrix} \frac{\partial(q_1x_1+q_2x_2+q_3x_3+\cdots+q_nx_n)}{x_1}\\ \frac{\partial(q_1x_1+q_2x_2+q_3x_3+\cdots+q_nx_n)}{x_2}\\ \frac{\partial(q_1x_1+q_2x_2+q_3x_3+\cdots+q_nx_n)}{x_3}\\ \vdots\\ \frac{\partial(q_1x_1+q_2x_2+q_3x_3+\cdots+q_nx_n)}{x_n} \end {bmatrix} } = {\begin{bmatrix} q_1\\ q_2\\ q_3\\ \vdots\\ q_n \end{bmatrix} } = q$

在这里我们可以写一下全微分的形式，便于后面的理解：

$dy=\frac{\partial y}{\partial x_1}dx_1+\frac{\partial y}{\partial x_2}dx_2+\frac{\partial y}{\partial x_3}dx_3+\cdots+\frac{\partial y}{\partial x_n}dx_n=\left(\frac {\partial y}{\partial x}\right)^Tdx$

由偏导数组合而成的向量 $q$ 是这个函数 $y$ 的梯度向量。梯度向量 $q$ 和自变量的微分量 $dx$ 的内积就是 $y$ 的微分量。为了统一形式，我们不如就约定，梯度向量都写成列向量。

向量对向量求导

从标量对向量求导推广到向量对向量求导就很简单了。从上面的一次内积推广到多次内积，结果以列向量表示。

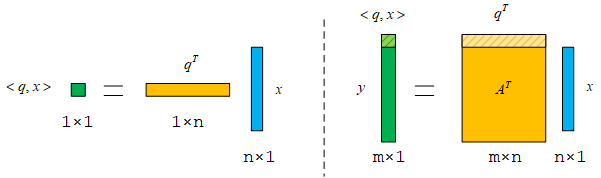
这时候列向量 $y$ 对列向量 $x$ 求偏导的结果应该为A，这样能够和前面的结论保持一致。

$\frac {\partial y}{\partial x}=\frac {\partial A^Tx}{\partial x}=A$

矩阵 $A$ 具体应该怎么求呢？应该 $y$ 的分量横着写，然后竖着写每个分量对 $x$ 的偏导数，这样子 $A$ 中每一列都是一个梯度向量。

海森（Hessian）矩阵

掌握了上面的求导方式之后，就可以求海森矩阵了。海森矩阵是多元函数的二阶偏导数构成的方阵。这里引入一个梯度算符“ $\nabla$ ”，求多元函数 $f(x)$ 的梯度向量可以用“ $\nabla_x f$ ”表示， $f(x)$ 的海森矩阵就是“ $\nabla_x ^2f$ ”。

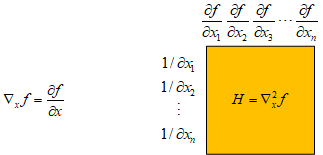
求导法则

上面介绍了两个重要的公式 $\partial {q^T}x/\partial x =\partial {x^T}q/\partial x= q$ 和 $\partial {A^T}x/\partial x = A$ ，在很多要求梯度的情况下都可以用这个这两个公式，再结合线性求导法则，乘法求导法则，链式求导法则，基本上就不会有大问题了。

$\frac {\partial \left(c_1f(x)+c_2g(x)\right)}{\partial x}=c_1\frac{\partial f(x)}{\partial x}+c_2\frac{\partial g(x)}{\partial x}$

$\frac{\partial (f(x)g(x))}{\partial x}=\frac{\partial f(x)}{\partial x}g(x)+f(x)\frac{\partial g(x)}{\partial x}$

这两条法则分别是线性求导法则和乘法求导法则，这个在标量对标量求导时适用，在对向量求导时也同样适用，大家肯定都比较熟悉了。但是链式求导法则和我们以前的经验有一点不一样，以前不需要注意左右顺序，但这里需要。
前面我们写过一个全微分式子，就是 $dy=(\partial y/\partial x)^Tdx$ 。从这里能够看到，要求梯度向量 $\partial y/\partial x$ 还可以通过先写全微分表达式，然后再对微分变量 $dx$ 前面的向量/矩阵转置来得到。我们可以用这个结论来推导链式求导法则。设 $y=f(g(x))$ ，求 $\partial y/\partial x$ ，先写我们已知的结论：

$dy=\left(\frac{\partial y}{\partial x}\right)^Tdx$

设 $u=g(x)$ ，写出全微分关系式：

$dy = {\left( {\frac{ {\partial y} }{ {\partial u} } } \right)^T}du\;\;\;\;du = {\left( {\frac{ {\partial u} }{ {\partial x} } } \right)^T}dx \to dy = {\left( {\frac{ {\partial y} }{ {\partial u} } } \right)^T}{\left( {\frac{ {\partial u} }{ {\partial x} } } \right)^T}dx$

上面的式子的含义就是 $x$ 的微小变化与 $u$ 对 $x$ 的梯度向量的内积可以得到 $u$ 的微小变化； $u$ 的微小变化与 $y$ 对 $u$ 的梯度向量的内积可以得到 $y$ 的微小变化。对比上面两个式子可以得出：

$\frac{ {\partial y} }{ {\partial x} } = {\left( { { {\left( {\frac{ {\partial y} }{ {\partial u} } } \right)}^T}{ {\left( {\frac{ {\partial u} }{ {\partial x} } } \right)}^T} } \right)^T} = \frac{ {\partial u} }{ {\partial x} }\frac{ {\partial y} }{ {\partial u} }$

如果函数嵌套的层数更多，结果也是类似的，函数从里往外依次求偏导，得到的结果依次从左往右相乘。如果不注意左右顺序，矩阵维度就无法对应。

2022年3月27日补充

标量对矩阵求导

类似标量对向量求导，求导结果与自变量是相同的维度。

$dy = <{ {\partial y} \over {\partial x} },dx > = {\left( { { {\partial y} \over {\partial x} } } \right)^T}dx$

标量对矩阵求导也应当是类似的形式。比如有一个m×n的矩阵 $W$ 和一个标量 $s$ ，它们之间满足这样的关系：

$ds = < { {\partial s} \over {\partial W} },dW > = {\mathop{\rm tr}\nolimits} \left( { { {\left( { { {\partial s} \over {\partial W} } } \right)}^T}dW} \right)$

$dW$ 和 ${\partial s} / {\partial W}$ 都是m×n的矩阵，我们用迹函数来表示矩阵内积。迹函数有一个特殊的性质：

${\mathop{\rm tr}\nolimits} (ABC) = {\mathop{\rm tr}\nolimits} (BCA) = {\mathop{\rm tr}\nolimits} (CAB)$

三个矩阵 $A$ 、 $B$ 、 $C$ 相乘得到一个方阵，它们循环移位后再相乘，不会改变结果的迹。之所以要求循环移位，是要让矩阵之间相乘的维度能够对应上。具体证明过程……我也不清楚，但是举几个简单的例子试一下会发现它确实是成立的。

向量对矩阵求导

如果顺着上面的思路来，向量对矩阵求导，就是向量中的每个分量对矩阵求导再组合在一起，这将是一个三维的张量。但有时候我们又会发现，比如 $s=Wx$ ，向量 $s$ 中的分量并不是和矩阵 $W$ 中的每个分量都有关的，如果按照前面的思路来，得到的将会是一个稀疏的结果。更直观的感觉可能是 $s$ 对 $W$ 求偏导应该得到一个向量，因为 $s$ 是由矩阵 $W$ 和向量 $x$ 相乘得到的。
遇到这种情况我觉得还是得具体问题具体分析，一般写成微分的形式肯定没问题，然后可以代入其他地方进行计算。

$ds = (dW)x$

岭回归

机器学习中的“回归”是相对于“分类”来说的，回归用于预测连续值，这里有点类似于数学上的拟合。
设有一组样本 $X$ 和样本对应的标签 $y$ 。 $X$ 中每一行是一个样本，每个样本在标签 $y$ 中有一个对应的结果。我们的目的是找到样本 $X$ 和标签 $y$ 的一组线性关系，使样本 $x_i$ 经过线性运算的结果能尽可能接近标签值 $y_i$ 。

${\omega _1}{x_{i1} } + {\omega _2}{x_{i2} } + {\omega _3}{x_{i3} } + \cdots + {\omega _n}{x_{in} } \to {y_i}$

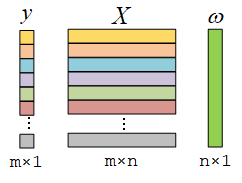
所以问题实际上是结合已有的数据求最优的系数 $\omega$ ，最常见的做法是最小二乘法，最小二乘法的目的是使计算结果和标签的平方误差最小。而岭回归是在最小二乘法基础上引入了正则项，防止过拟合，提高了计算的稳定性。
写出目标函数 $\mathcal L$ ，优化 $\omega$ 来令目标函数最小化。

$\mathop {\min }\limits_\omega \mathcal L=||y-X\omega||^2+\lambda||\omega||^2$

类似一元二次函数，令梯度向量为零向量可以取到 $\mathcal L$ 的最小值。

$\frac{ {\partial {\mathcal L} } }{ {\partial \omega } } = \frac{ {\partial \left( { { {\left( {y - X\omega } \right)}^T}\left( {y - X\omega } \right) + \lambda {\omega ^T}\omega } \right)} }{ {\partial \omega } } = - {X^T}2(y - X\omega ) + 2\lambda \omega = 0$

上面的求导过程用了链式求导法则、乘法求导法则和线性求导法则。整理之后可以得到：

$\omega = \left( { {X^T}X + \lambda I} \right)^{-1}{X^T}y$

相比于最小二乘法，岭回归的结果多了 $\lambda I$ ，就像是一条山“岭”加在方阵 $X^TX$ 上，所以起名叫“岭回归”。原先最小二乘法计算过程中有可能 $X^TX$ 不是满秩，无法求逆。现在加上了 $\lambda I$ 就一定能求逆了，所以提高了计算的稳定性。
这里看上去只能求样本和标签的线性关系，但如果 $x_i$ 的分量中用的是多项式、指数函数、三角函数等，它也能够用来求解。这时候是将结果用一些多项式或者初等函数的线性组合来描述，不同的拟合方式取决于构建的模型。

表示定理（Representer Theorem）

表示定理是对偶空间的精髓所在。

考虑一个线性回归问题：

$\mathop {\min }\limits_\omega \sum\limits_i^m {L({\omega ^T}{x_i},{y_i})} + \lambda ||\omega |{|^2}$

表示定理所描述的问题相比于岭回归更加一般化，这里的误差函数也是任意的，而岭回归用的是最小平方误差。
$\omega$ 和 $x$ 是相同维度n的向量，总共有m个样本，设 $\omega = \omega_\parallel+\omega_\bot$ ，其中 $\omega_\parallel$ 存在于所有样本 $x_i$ 张成的子空间，就是说 $\omega_\parallel$ 可以用所有样本来线性表示；而 $\omega_\bot$ 则是和每个样本都垂直， $\omega_\bot$ 和每个样本的内积都是0。

${\omega_\parallel } = \sum\limits_i^m { {\alpha _i}{x_i} } \;\;\;\;\;\;\;{\omega_ \bot }^T{x_i} = 0$

这里的 $\alpha$ 存在于对偶空间， $\omega$ 存在于源空间。

这样的分解一定是合理的， $\omega_\parallel$ 存在于样本的生成子空间，而 $\omega_\bot$ 存在于这个生成子空间的直和补子空间。它们俩的和可以用来表示全空间中的任意向量。把它们代入原问题中：

$\mathop {\min }\limits_\omega \sum\limits_i^m {L(\omega_\parallel ^T{x_i} + \omega _\bot ^T{x_i},{y_i})} + \lambda ||{\omega_\parallel } + {\omega _\bot }|{|^2} = \mathop {\min }\limits_\omega \sum\limits_i^m {L(\omega _\parallel ^T{x_i},{y_i})} + \lambda ||{\omega_\parallel }|{|^2} + \lambda ||{\omega _\bot }|{|^2}$

这个最小化问题，肯定希望 $||\omega_\bot||^2$ 越小越好； $\omega$ 的最优解，肯定是在 $\omega_\bot=\bold 0$ 的时候取到。所以 $\omega=\omega_\parallel$ 。有了这个先验条件之后，我们再回过头去看岭回归。

$\omega = \left( { {X^T}X + \lambda I} \right)^{-1}{X^T}y=X^T\alpha$

这里用 $X^T\alpha$ 表示样本的线性组合，因为 $X$ 中的样本是一行一行放置的。

求解 $\alpha$ ：

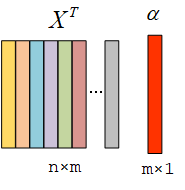
$\begin{array}{l} \left( { {X^T}X + \lambda I} \right){X^T}\alpha = {X^T}y\\ {X^T}\left( {X{X^T} + \lambda I} \right)\alpha = {X^T}y\\ \alpha = {\left( {X{X^T} + \lambda I} \right)^{ - 1} }y \end{array}$

再理一下我们求解的思路。前面的岭回归其实运算量比较大，涉及大量矩阵运算。现在在求 $\omega$ 之前引入一个中间变量 $\alpha$ ，让问题一下子简单了很多。

降低维度

$XX^T$ 就是我在上一篇文章中提到的Gram矩阵，矩阵中的元素是样本两两之间的内积。求 $\alpha$ 是一个m维的运算，m是样本的个数。然后将 $\alpha$ 作为系数，对样本线性求和就能够得到 $\omega$ 。
这个在样本维度n非常大的时候非常有用，很多情况下我们会把样本映射到高维的特征空间，维度n往往会远大于样本个数m，这时候用这个方法求解就一下子把n维的问题降到m维！

将问题归结为内积运算

而且它也不需要显式地求出 $\omega$ 。比如当我们训练完成，然后输入新的一个样本 $z$ 。

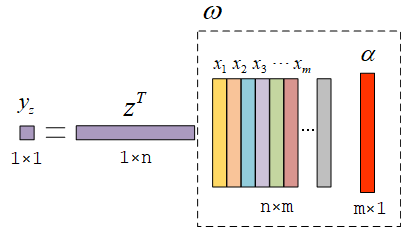
${y_z} = {z^T}{X^T}\alpha = \left[ {\begin{matrix} { {z^T}{x_1} }&{ {z^T}{x_2} }&{ {z^T}{x_3} }& \cdots &{ {z^T}{x_m} } \end{matrix} } \right]\alpha$

所以不管是训练的时候求 $\alpha$ ，还是输入新的样本进行推断，用到的都只是样本的内积，我们不用再去关心 $\omega$ 的具体形式。如果能有一个快速计算高维样本内积的方法就好了，这就用到了核函数。

核函数

核函数的引入实际上是通过一个 $\varphi(x)$ 将低维的样本向量 $x$ 映射到高维空间，这个高维空间一般称为特征空间。引入核函数以后，只是样本的维度增加了，对解的结构没有影响。核函数一般用 $\kappa (u,v)$ 表示。

$\kappa (u,v) = \varphi {(u)^T}\varphi (v)$

它可以方便地计算 $\varphi(u)$ 与 $\varphi(v)$ 在高维空间的内积。而样本到了高维空间之后就有可能解决之前低维空间无法分类的问题。
所以在多了核函数以后，只是我们处理的样本维度变了，解的整体结构还是没有变，只要把前面求内积的地方换成核函数就好了。
带核函数的岭回归训练结果：

$\alpha = {\left( {K + \lambda I} \right)^{ - 1} }y\;\;\;\;\;{K_{ij} } = \kappa ({x_i},{x_j})$

带核函数的岭回归前向推断：

${y_z} = \left[ {\begin{matrix} \kappa (z,x_1)&\kappa (z,x_2)&\kappa (z,x_3)& \cdots &\kappa (z,x_m) \end{matrix} } \right]\alpha$

P.S.关于对偶空间的解释

引用作者博士论文里的一张图，感觉解释得比较直观。