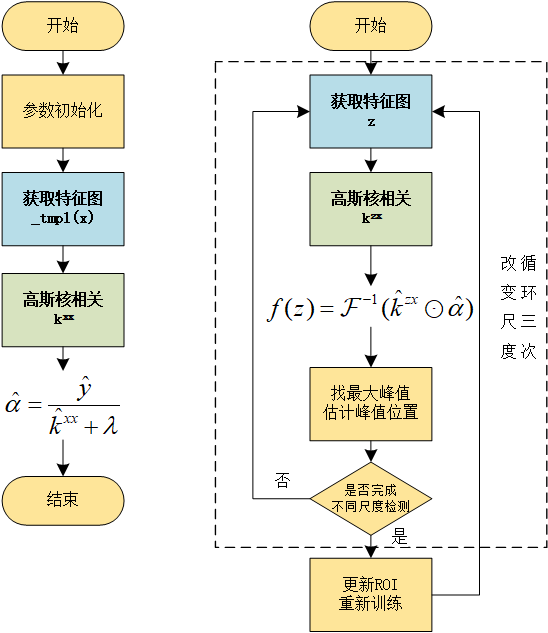
本文是CSK与KCF算法推导的第三篇，主要介绍算法的主体部分推导。

循环矩阵

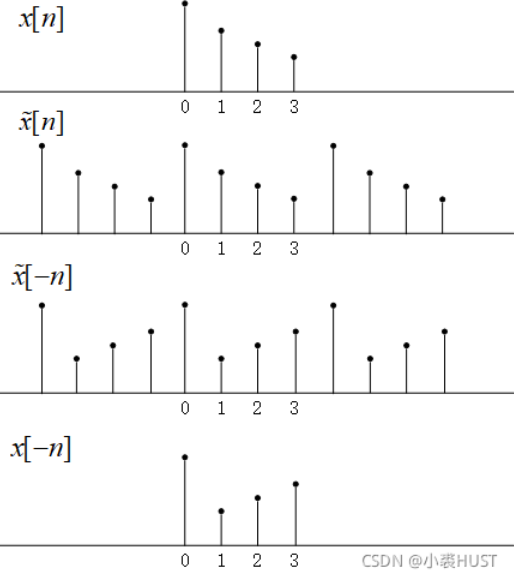
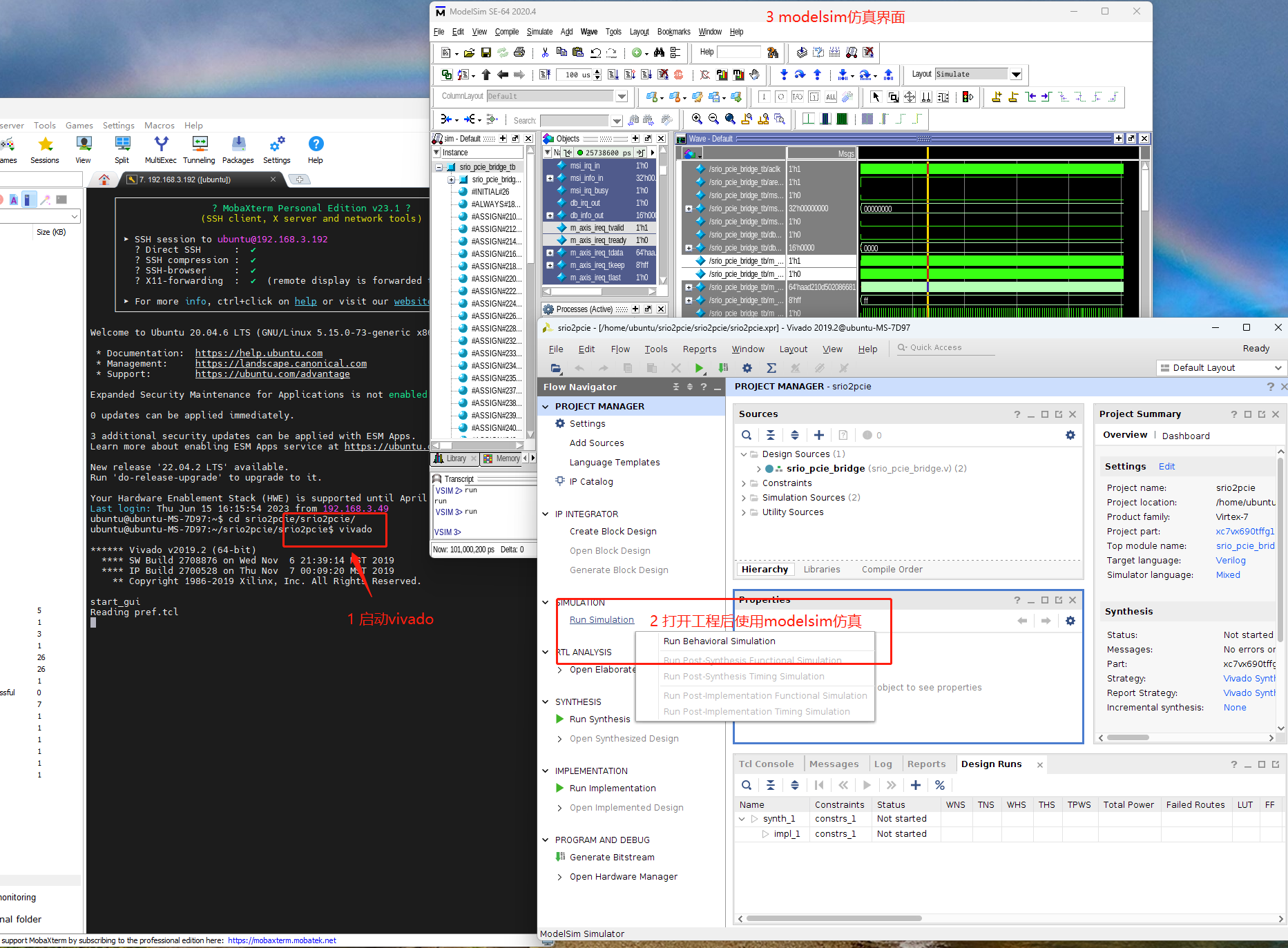
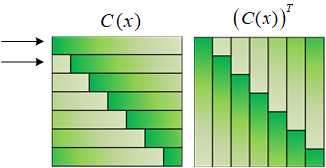
  循环矩阵从CSK的文章里就提出了，概念也很容易理解。一个样本xx，可以通过循环移位生成不同的向量，组合成一个矩阵C(x)C(x)。下面的图里分别列出了xx、C(x)C(x)和C(x)C(x)的转置。

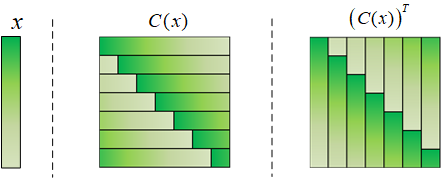
  循环矩阵C(x)C(x)和另一个列向量zz相乘，得到的结果就是xx和zz进行相关运算的结果。这个也很好理解，就是xx在zz上面滑动，然后进行乘加运算。同样可以写出循环卷积的矩阵表达式，循环卷积需要先将xx倒序，然后再滑动。对比循环卷积所用的矩阵和(C(x))T(C(x))^T的颜色，可以发现它们俩是一样的！

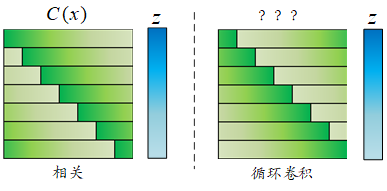
  循环矩阵C(x)C(x)既然能和循环卷积联系起来了，那么自然可以想到把DFT矩阵也联系起来。这就能得出一个重要的结论：循环矩阵C(x)C(x)能够用DFT矩阵对角化！
  下面是证明过程。先根据时域卷积等于频域乘积写出等式：

(C(x))Tz=x∗z=F−1(x^⊙z^){\left( {C(x)} \right)^T}z = x*z = { {\mathcal F}^{ - 1} }(\hat x \odot \hat z)

  其中“⊙\odot”是哈达玛积（Hadamard product），或者称为“element-wise product”，表示两个向量对应位置的分量直接相乘。x^\hat x和z^\hat z分别表示xx和zzDFT变换之后的序列。

(C(x))Tz=1sFH(x^⊙Fz)=1sFHdiag(x^)Fz{\left( {C(x)} \right)^T}z = \frac{1}{s}{F^H}(\hat x \odot Fz) = \frac{1}{s}{F^H}diag(\hat x)Fz

  两个列向量的哈达玛积可以转换成对角矩阵和列向量相乘。diag(x^)diag(\hat x)表示把x^\hat x放到对角线上形成对角矩阵。因为上式对所有的zz都成立，所以可以去掉zz，得到：

(C(x))T=1sFHdiag(x^)FC(x)=(1sFT)diag(x^)(1sF∗)\begin{array}{l} {\left( {C(x)} \right)^T} = \frac{1}{s}{F^H}diag(\hat x)F\\ C(x) = \left( {\frac{1}{ {\sqrt s } }{F^T} } \right)diag(\hat x)\left( {\frac{1}{ {\sqrt s } }{F^*} } \right) \end{array}

  又因为F=FTF=F^T，且U=1sFU={\frac{1}{ {\sqrt s } }F}是酉矩阵。C(x)C(x)可以进一步表示为：

C(x)=Udiag(x^)U∗C(x) = Udiag(\hat x){U^*}

  这个结论就非常厉害了。所有循环矩阵都可以特征分解，特征值是原始序列的DFT；所有循环矩阵的特征向量都相同。这就为后面的运算带来了很大的便利。
  上面的推导是从循环卷积的角度出发的，而我在第一篇文章中还写了相关运算与DFT的关系。

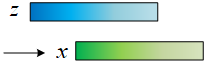
  这里的相关运算相当于是xx相对于zz在向右滑动，所以xx的DFT结果需要取复共轭，可以这样表示结果：

C(x)z=x⋆z=F−1(x^∗⊙z^){ {C(x)z = x} } \star z = { {\mathcal F}^{ - 1} }({ {\hat x}^*} \odot \hat z)

  其中⋆\star表示相关运算，经过类似的推导之后可以得到：

C(x)=U∗diag(x^∗)UC(x) = U^*diag(\hat x^*){U}

循环移位的意义

  一方面原因已经在上面推导，循环矩阵能够用DFT对角化。另一方面要清楚输入样本xx并不都是我们关心的目标。我们关心的Target只有其中的一部分，就如下面的图所示。

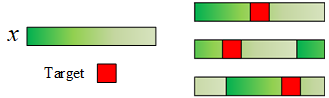
  这么做就能够在训练的时候为我们关心的Target提供一些上下文（context）信息。xx在循环移位的过程中确实起到了“密集采样”的作用。

生成标签

  在生成标签的时候我们可以给原始样本xx一个较大的标签值，其他由循环移位产生的样本给较小的标签值，相对位移越大，标签值越小。

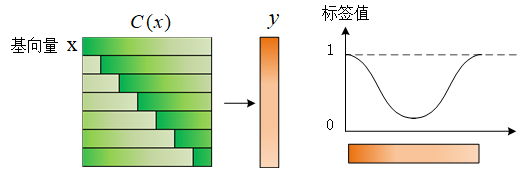
  因为是循环移位，所以移位越接近一个周期，这个样本越接近正样本。所以样本的标签值是一个峰值在两侧的高斯函数。

训练（不带核函数）

  样本训练还是用的岭回归。结合第二篇文章，虽然在引入核函数之后，我们就不关心ω\omega是多少了，但在没有引入核函数的时候，能求出ω\omega自然更好。

ω=(XTX+λI)−1XTy\omega = {\left( {X^TX + \lambda I} \right)^{ - 1} }X^Ty

  只需要将样本矩阵XX替换成C(x)C(x)即可。上面的表达式里用的是转置而不是共轭转置，因为我们前面的推导是在实数的条件下得到的，因为这对于我们分析问题来说已经足够了。
  有人可能会担心，C(x)C(x)分解之后的三个矩阵都是复矩阵，这里是不是应该用共轭转置啊？要用共轭转置很简单，把前面岭回归的推导用共轭转置推导一遍就行，这里的转置是可以推广到共轭转置的。但其实也可以就只用转置，因为这里的C(x)C(x)本质上还是实数矩阵，转置是能够成立的。我们已经在前面已经有两个关于C(x)C(x)的分解了，可以都用来帮助化简。把X=C(x)X=C(x)代入：

ω=(UTdiag(x^∗)UHUdiag(x^)U∗+λI)−1UTdiag(x^∗)UHy\omega = {\left( { {U^T}diag({ {\hat x}^*}){U^H}Udiag(\hat x){U^*} + \lambda I} \right)^{ - 1} }{U^T}diag({ {\hat x}^*}){U^H}y

  把握几个关键点，UHU=UUH=U∗U=UU∗=IU^HU=UU^H=U^*U=UU^*=I；对角矩阵相乘就是对角线上元素的对应相乘；对角矩阵转置就是对角线上元素求倒数；(ABC)−1=C−1B−1C−1(ABC)^{-1}=C^{-1}B^{-1}C^{-1}；Ux=x^/sUx=\hat x/\sqrt s；U∗x=x^∗/sU^*x=\hat x^*/\sqrt s。

ω=(UTdiag(x^∗)UHUdiag(x^)U∗+λI)−1UTdiag(x^∗)UHy    =Udiag(1x^∗⊙x^+λ)U∗Udiag(x^∗)U∗y    =Udiag(x^∗x^∗⊙x^+λ)U∗y\begin{array}{l} \omega = {\left( { {U^T}diag({ {\hat x}^*}){U^H}Udiag(\hat x){U^*} + \lambda I} \right)^{ - 1} }{U^T}diag({ {\hat x}^*}){U^H}y\\ \ \ \ \ = Udiag\left( {\frac{1}{ { { {\hat x}^*} \odot \hat x + \lambda } } } \right){U^*}Udiag({ {\hat x}^*}){U^*}y\\ \ \ \ \ = Udiag\left( {\frac{ { { {\hat x}^*} } }{ { { {\hat x}^*} \odot \hat x + \lambda } } } \right){U^*}y \end{array}

  这里diagdiag里面的计算都是element-wise的。

U∗ω=diag(x^∗x^∗⊙x^+λ)U∗y{U^*}\omega = diag\left( {\frac{ { { {\hat x}^*} } }{ { { {\hat x}^*} \odot \hat x + \lambda } } } \right){U^*}y

ω^∗=x^∗⊙y^∗x^∗⊙x^+λ{ {\hat \omega }^*} = \frac{ { { {\hat x}^*} \odot { {\hat y}^*} } }{ { { {\hat x}^*} \odot \hat x + \lambda } }

  最后的化简结果如下。相比于原先复杂的矩阵运算，现在只需要少量DFT、IDFT和element-wise的运算即可。

ω^=x^⊙y^x^∗⊙x^+λ\hat \omega = \frac{ {\hat x \odot \hat y} }{ { { {\hat x}^*} \odot \hat x + \lambda } }

  这个地方的推导也是知乎上有人提出推导有误的地方。原文中的结果里面分子的x^\hat x多了复共轭，因为在原文的公式（55）处落下了一个复共轭。而这部分结果作者也没有用到具体算法中，所以对算法没有影响。

训练（带核函数）

  带核函数的情况下，我们就不用求ω\omega了，只要求中间变量α\alpha就好了。

α=(K+λI)−1y\alpha = {\left( {K + \lambda I} \right)^{ - 1} }y

  计算Gram矩阵

  逐行观察上面的矩阵乘法，就看前两行就行。可以发现这两行的结果也是一个相对移位的关系。所以当样本矩阵是循环矩阵的时候，这一组样本的Gram矩阵也会是循环矩阵。而循环的基向量就是Gram矩阵的第一行。KK是高维空间的Gram矩阵，这一结论自然也成立，KK也是一个循环矩阵。

K=C(kxx)        kxx=[κ(x,P0x)κ(x,P1x)κ(x,P2x)⋯κ(x,Pnx)]K = C({k^{xx} })\;\;\;\;{k^{xx} } = \left[ {\begin{matrix} {\kappa (x,P^0x)}&{\kappa (x,P^1x)}&{\kappa (x,P^2x)}& \cdots &{\kappa (x,P^nx)} \end{matrix} } \right]

  这里的PP矩阵的作用是让列向量φ(x)\varphi(x)循环移位。比如P0P^0是不移位，P1P^1是循环移位1次，P2P^2是循环移位2次，以此类推。

α=(C(kxx)+λI)−1y=(Udiag(k^xx)U∗+λI)−1y\alpha = {\left( {C({k^{xx} }) + \lambda I} \right)^{ - 1} }y = {\left( {Udiag({ {\hat k}^{xx} }){U^*} + \lambda I} \right)^{ - 1} }y

U∗α=diag(1k^xx+λ)U∗y{U^*}\alpha = diag\left( {\frac{1}{ { { {\hat k}^{xx} } + \lambda } } } \right){U^*}y

α^∗=y^∗k^xx+λ\hat \alpha^* = \frac{ {\hat y^*} }{ { { {\hat k}^{xx} } + \lambda } }

  用循环矩阵的形式表示KK，然后特征分解，利用对角矩阵和酉矩阵的特性即可完成上面的化简。这时候计算量相对比较大的地方就是求kxxk^{xx}了，它是向量xx和xx的循环移位的向量在高维空间的内积构成的向量。
  然后对上面的等式两边取复共轭，就可以得到：

α^=y^k^xx∗+λ\hat \alpha = \frac{ {\hat y} }{ { { { {\hat k}^{xx} }^*} + \lambda } }

  但这和论文里的结论不一样，论文里的结论，分母的k^xx{\hat k }^{xx}没有取复共轭。但实际上这里取复共轭或者不取复共轭都行，因为k^xx{\hat k }^{xx}是实数。
  什么样的实数序列做DFT之后还能是实数？观察旋转因子WNknW_N^{kn}，旋转因子在复平面上的分布就是有对称性的，当实数序列满足一定条件之后，虚部就能够抵消。

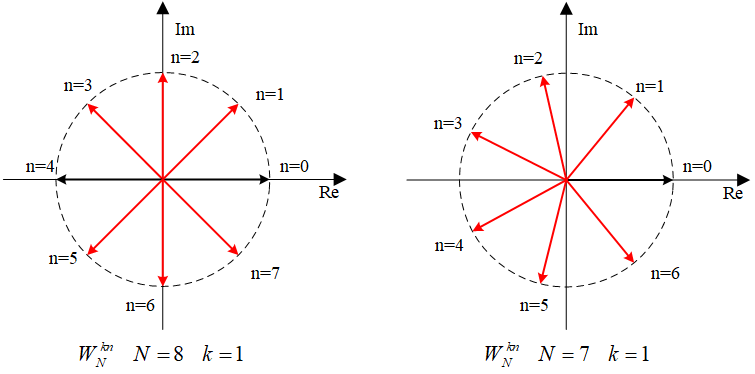
  观察可以发现，只要序列满足x[i]=x[N−i]   i=1,2,...,N−1x[i] = x[N-i]\ \ \ i=1,2,...,N-1这个条件，这些旋转因子的虚部就都能够被抵消。对于二维的图像来说，就是我们不关心它的第0行和第0列，第0行和第0列可以是任意实数，然后剩余的数据是中心对称的就可以。
  序列xx的自相关kxxk^{xx}自然就满足这一条件。所以更一般的结果还可以是：

α^=y^real(k^xx)+λ\hat \alpha = \frac{ {\hat y} }{ { {real({ {\hat k}^{xx} })} + \lambda } }

  我们还可以让结果更简单，就是如果yy给定的标签同样满足上面的条件，那么y^\hat y就也是一个实数。这样整个α^\hat \alpha也是实数了！！

α^=real(y^)real(k^xx)+λ\hat \alpha = \frac{real({\hat y})}{ { {real({ {\hat k}^{xx} })} + \lambda } }

  通过上面的计算，我们还可以想到一个结论，K=C(kxx)K = C({k^{xx} })不光是一个循环矩阵，也还是一个对称矩阵，K=KTK=K^T。结合这一结论我们可以重新进行一次推导：

α=(KT+λI)−1y\alpha = {\left( { {K^T} + \lambda I} \right)^{ - 1} }y

α=(C(kxx)T+λI)−1y=(U∗diag(k^xx)U+λI)−1y\alpha = {\left( {C({k^{xx} })^T + \lambda I} \right)^{ - 1} }y = {\left( {U^*diag({ {\hat k}^{xx} }){U} + \lambda I} \right)^{ - 1} }y

Uα=diag(1k^xx+λ)Uy{U}\alpha = diag\left( {\frac{1}{ { { {\hat k}^{xx} } + \lambda } } } \right){U}y

α^=y^k^xx+λ\hat \alpha = \frac{ {\hat y} }{ { { {\hat k}^{xx} } + \lambda } }

  这样就能直接得到论文中给出的结论。

带核函数的检测

  检测就是我们的训练完成之后送进一个新的样本zz来预测输出。不带核函数的情况下因为直接计算出了ω\omega，所以只需要求ω\omega和zz的内积就能得到结果。带核函数的情况在上一篇文章中介绍了，不需要显式地求出ω\omega，只需要将输入样本zz和所有训练样本做内积，得到一个维度是样本个数的列向量，然后把这个列向量和α\alpha做内积即可得到一个预测结果。
  逐个样本zz进行检测太慢了，我们把zz也扩展成循环矩阵C(z)C(z)，然后就可以直接做一批样本的检测，这一批样本相互之间是空间上的位移关系，最后得到f(z)f(z)是一个列向量，表示一批样本的检测结果。

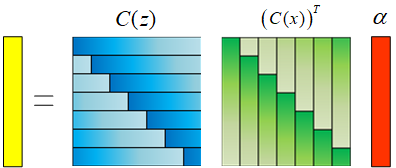
  在没有引入核函数的情况下，上面的C(z)C(z)和(C(x))T(C(x))^T相乘得到的也是一个循环矩阵。引入核函数之后，每个样本都经过φ(x)\varphi(x)映射到高维空间。我们把高维空间的C′(z)C'(z)和(C′(x))T(C'(x))^T相乘的结果记作KzK^z

Kz=C(kzx)        kzx=[κ(z,P0x)κ(z,P1x)κ(z,P2x)⋯κ(z,Pnx)]K^z = C({k^{zx} })\;\;\;\;{k^{zx} } = \left[ {\begin{matrix} {\kappa (z,P^0x)}&{\kappa (z,P^1x)}&{\kappa (z,P^2x)}& \cdots &{\kappa (z,P^nx)} \end{matrix} } \right]

  把结果用循环矩阵化简：

f(z)=C(z)(C(x))Tα=Kzα=C(kzx)α=Udiag(k^zx)U∗αf(z) = C(z){\left( {C(x)} \right)^T}\alpha = {K^z}\alpha = C({k^{zx} })\alpha = Udiag({\hat k^{zx} }){U^*}\alpha

U∗f(z)=diag(k^zx)U∗α{U^*}f(z) = diag({ {\hat k}^{zx} }){U^*}\alpha

f^∗(z)=k^zx⊙a^∗{ {\hat f}^*}(z) = { {\hat k}^{zx} } \odot { {\hat a}^*}

  这里的结果和论文中的结果有点不一样，这是因为KzK^z的表示方式不太一样，原文中用的是f(z)=(Kz)Tαf(z)=(K^z)^T\alpha，所以Kz=C(x)(C(z))TK^z=C(x)\left (C(z) \right)^T

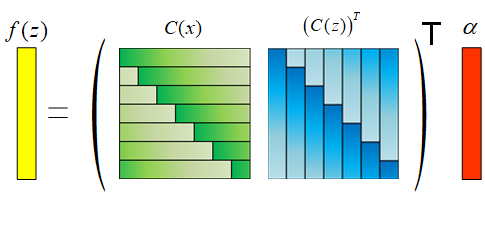
Kz=C(kxz)        kxz=[κ(x,P0z)κ(x,P1z)κ(x,P2z)⋯κ(x,Pnz)]K^z = C({k^{xz} })\;\;\;\;{k^{xz} } = \left[ {\begin{matrix} {\kappa (x,P^0z)}&{\kappa (x,P^1z)}&{\kappa (x,P^2z)}& \cdots &{\kappa (x,P^nz)} \end{matrix} } \right]

  把结果用循环矩阵化简：

f(z)=(Kz)Tα=(C(kxz))Tα=U∗diag(k^xz)Uαf(z) = ({K^z})^T\alpha = (C({k^{xz} }))^T\alpha = U^*diag({\hat k^{xz} }){U}\alpha

Uf(z)=diag(k^xz)Uα{U}f(z) = diag({ {\hat k}^{xz} }){U}\alpha

f^(z)=k^xz⊙a^{ {\hat f} }(z) = { {\hat k}^{xz} } \odot { {\hat a} }

  这两个结论的区别在于求xx和zz的互相关时，两个序列的相对滑动方向不一样。结合我的第一篇文章中关于相关运算用DFT加速的内容：

k^zx=z^⊙x^∗{\hat k}^{zx} = \hat z \odot{\hat x}^*

k^xz=x^⊙z^∗{\hat k}^{xz} = \hat x \odot{\hat z}^*

  我更倾向于使用后者的结论，那样在没有引入核函数的情况下计算f(z)f(z)可以表示为：

f(z)=F−1(x^⊙z^∗⊙α^)f(z)={\mathcal F}^{-1}(\hat x \odot{\hat z}^*\odot\hat \alpha)

核函数计算

  有些核函数的计算也可以利用循环矩阵来加速。

多项式核

κ(u,v)=(uTv+a)b\kappa(u,v)=(u^Tv+a)^b

  在训练的时候计算kxxk^{xx}，uu和vv一个始终是原始样本xx，另一个是循环移位的样本。这就是自相关运算，所以可以用DFT来加速。

kixx=κ(x,Pix)=(xTPix+a)b=(F−1(x^⊙x^∗)+a)bk_i^{xx} = \kappa (x,{P^i}x) = {({x^T}{P^i}x + a)^b} = {\left( { { {\mathcal F}^{ - 1} }(\hat x \odot { {\hat x}^*}) + a} \right)^b}

  在检测的时候计算kxzk^{xz}。这时候是互相关运算，互相关运算要注意它们相对滑动的方向，然后再确定哪个需要取复共轭。

kixz=κ(z,Pix)=(zTPix+a)b=(F−1(x^⊙z^∗)+a)bk_i^{xz} = \kappa (z,{P^i}x) = {({z^T}{P^i}x + a)^b} = {\left( { { {\mathcal F}^{ - 1} }(\hat x \odot { {\hat z}^*}) + a} \right)^b}

高斯核

κ(u,v)=exp(−1σ2∣∣u−v∣∣2)\kappa (u,v) = exp\left( { - \frac{1}{ { {\sigma ^2} } }||u - v|{|^2} } \right)

  在训练的时候计算kxxk^{xx}。

kixx=κ(x,Pix)=exp(−2σ2(∣∣x∣∣2−F−1(x^⊙x^∗)))k_i^{xx} = \kappa (x,{P^i}x) = exp\left( { - \frac{2}{ { {\sigma ^2} } }\left( {||x|{|^2} - { {\mathcal F}^{ - 1} }(\hat x \odot { {\hat x}^*})} \right)} \right)

  在检测的时候计算kxzk^{xz}。

kixz=κ(x,Pix)=exp(−1σ2(∣∣x∣∣2+∣∣z∣∣2−2F−1(x^⊙z^∗)))k_i^{xz} = \kappa (x,{P^i}x) = exp\left( { - \frac{1}{ { {\sigma ^2} } }\left( {||x|{|^2} + ||z|{|^2} - 2{ {\mathcal F}^{ - 1} }(\hat x \odot { {\hat z}^*})} \right)} \right)