本文是CSK与KCF算法推导的第五篇,主要介绍具体实现的细节。
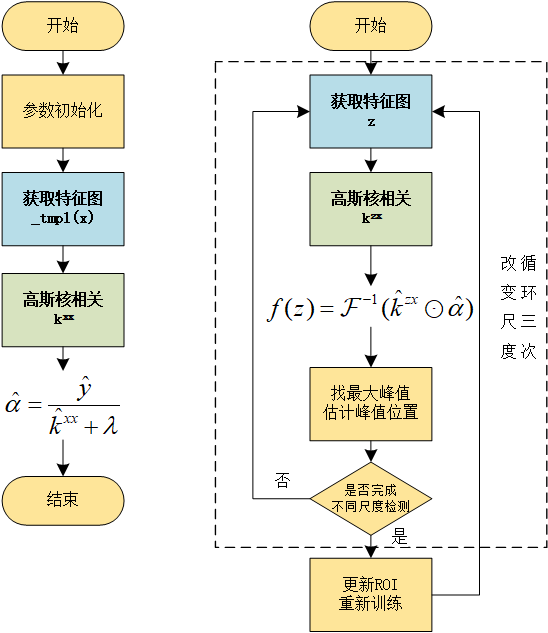
算法流程
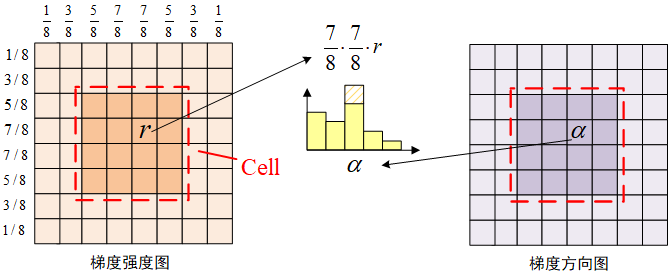
算法的大致流程如上图所示。左边是第一次训练,右边是每次的更新。我认为整个算法最关键的地方在于提取特征图 和核函数的计算 。作者的代码里有提取hog特征,也有直接用原始的灰度图像数据作为特征图,目前我只看了用灰度图作为特征图的部分。需要注意的是,这里的灰度图是归一化到[-0.5,0.5]的区间内的!!!
fftshift()
MATLAB里有一个fftshift()的函数。原本DFT的结果中,低频部分是在序列两端,高频在中间;这个函数可以把低频移到中间,高频移到两边。
在我前面的文章中介绍了,标签值应该是一个峰值在序列两端的高斯函数。既然我们是用这样的标签训练的,我们在检测的时候,如果检测一个和训练样本类似的样本,那么得到的结果也会是一个峰值在两端的结果。这时候可以用类似fftshift()的函数将结果重新排布一下,这样能便于分析。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 cv::Mat KCFTracker::createGaussianPeak (int sizey, int sizex) { cv::Mat_<float > res (sizey, sizex) ; int syh = (sizey) / 2 ; int sxh = (sizex) / 2 ; float output_sigma = std ::sqrt ((float ) sizex * sizey) / padding * output_sigma_factor; float mult = -0.5 / (output_sigma * output_sigma); for (int i = 0 ; i < sizey; i++) for (int j = 0 ; j < sizex; j++) { int ih = i - syh; int jh = j - sxh; res(i, j) = std ::exp (mult * (float ) (ih * ih + jh * jh)); } return FFTTools::fftd(res); }
上面是作者采用的生成标签值的代码,可以看到这个生成得到标签值并没有符合峰值在四个角点的要求。但作者的代码确实是能用的,为什么呢?因为作者是在计算高斯核相关的时候做了fftshift。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 cv::Mat KCFTracker::gaussianCorrelation (cv::Mat x1, cv::Mat x2) { using namespace FFTTools; cv::Mat c = cv::Mat( cv::Size(size_patch[1 ], size_patch[0 ]), CV_32F, cv::Scalar(0 ) ); if (_hogfeatures) { …… } else { cv::mulSpectrums(fftd(x1), fftd(x2), c, 0 , true ); c = fftd(c, true ); rearrange(c); c = real(c); } ……
上面的rearrange()函数就是完成了fftshift()的功能。为什么能够这么做呢?
α ^ = y ^ k ^ x x + λ \hat \alpha = \frac{ {\hat y} }{ { { {\hat k}^{xx} } + \lambda } }
α ^ = k ^ xx + λ y ^
我们可以对作者代码中采用的计算方式做一个推导。记α ′ \alpha' α ′ y y y y ′ y' y ′
α ^ ′ = F ( y ′ ) F ( k x x ( x − N / 2 , y − M / 2 ) ) + λ = F ( y ( x − N / 2 , y − M / 2 ) ) F ( k x x ( x − N / 2 , y − M / 2 ) ) + λ \hat \alpha ' = \frac{ { {\mathcal F}(y')} }{ { {\mathcal F}\left( {k^{xx}(x - N/2,\;y - M/2)} \right){\rm{ + } }\lambda } }= \frac{ { {\mathcal F}(y(x - N/2,\;y - M/2))} }{ { {\mathcal F}\left( { {k^{xx} }(x - N/2,\;y - M/2)} \right){\rm{ + } }\lambda } }
α ^ ′ = F ( k xx ( x − N /2 , y − M /2 ) ) + λ F ( y ′ ) = F ( k xx ( x − N /2 , y − M /2 ) ) + λ F ( y ( x − N /2 , y − M /2 ))
二维fftshift()相当于是在矩阵行列方向上分别循环移位一半的长度。自然y y y y ′ y' y ′
α ^ ′ ( u , v ) = y ^ W N u N / 2 W M v M / 2 k ^ x x W N u N / 2 W M v M / 2 + λ = y ^ ( − 1 ) u + v k ^ x x ( − 1 ) u + v + λ \hat \alpha '(u,v) = \frac{ {\hat yW_N^{uN/2}W_M^{vM/2} } }{ { { {\hat k}^{xx} }W_N^{uN/2}W_M^{vM/2} + \lambda } } = \frac{ {\hat y{ {( - 1)}^{u + v} } } }{ { { {\hat k}^{xx} }{ {( - 1)}^{u + v} } + \lambda } }
α ^ ′ ( u , v ) = k ^ xx W N u N /2 W M v M /2 + λ y ^ W N u N /2 W M v M /2 = k ^ xx ( − 1 ) u + v + λ y ^ ( − 1 ) u + v
= y ^ ( − 1 ) u + v k ^ x x ( − 1 ) u + v + λ ( − 1 ) u + v = y ^ k ^ x x + λ = α ^ ( u , v ) = \frac{ {\hat y{ {( - 1)}^{u + v} } } }{ { { {\hat k}^{xx} }{ {( - 1)}^{u + v} } + \lambda { {( - 1)}^{u + v} } } } = \frac{ {\hat y} }{ { { {\hat k}^{xx} } + \lambda } } = \hat \alpha(u,v)
= k ^ xx ( − 1 ) u + v + λ ( − 1 ) u + v y ^ ( − 1 ) u + v = k ^ xx + λ y ^ = α ^ ( u , v )
所以作者代码中的做法是可行的。
峰值点估计
因为处理的图像的点都是离散的,所以我们在f ( z ) f(z) f ( z )
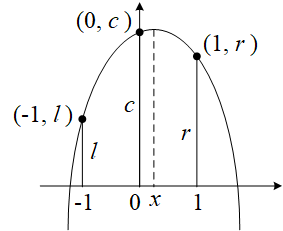
用检测到的峰值点和与它临近的两个点可以对真正的峰值点进行估计。用三个点来拟合二次函数,非常简单,设f ( x ) = a x 2 + b x + q f(x)=ax^2+bx+q f ( x ) = a x 2 + b x + q
{ a − b + q = l q = c a + b + q = r \left\{ \begin{array}{l}
a - b + q = l\\
q = c\\
a + b + q = r
\end{array} \right. ⎩ ⎨ ⎧ a − b + q = l q = c a + b + q = r
x = − b 2 a = − r − l 2 ( l + r − 2 c ) = r − l 2 ( 2 c − l − r ) x = - \frac{b}{ {2a} } = - \frac{ {r - l} }{ {2(l + r - 2c)} } = \frac{ {r - l} }{ {2(2c - l - r)} }
x = − 2 a b = − 2 ( l + r − 2 c ) r − l = 2 ( 2 c − l − r ) r − l
下面是作者采用的代码:
1 2 3 4 5 6 7 8 9 10 float KCFTracker::subPixelPeak (float left, float center, float right) { float divisor = 2 * center - right - left; if (divisor == 0 ) return 0 ; return 0.5 * (right - left) / divisor; }
峰值位置与目标位置
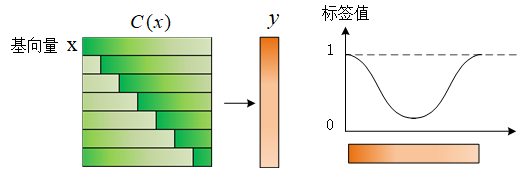
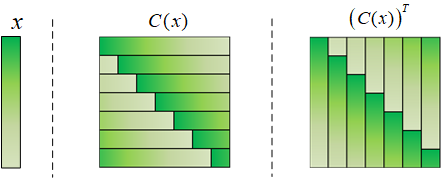
我们按照这样的样本C ( x ) C(x) C ( x ) y y y α \alpha α z z z
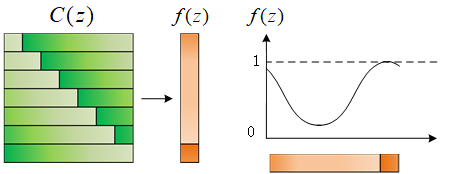
那么会得到怎样的响应呢?先把z z z f ( z ) f(z) f ( z ) 峰值点相对于标签值左移了一个单位,而样本则是右移一个单位 。
所以f ( z ) f(z) f ( z ) f ( z ) f(z) f ( z ) ( Δ x , Δ y ) (\Delta x,\ \Delta y) ( Δ x , Δ y ) ( − Δ x , − Δ y ) (-\Delta x,\ -\Delta y) ( − Δ x , − Δ y ) f ( z ) f(z) f ( z ) x [ − n ] = X ∗ [ k ] x[-n]=X^*[k] x [ − n ] = X ∗ [ k ] f ^ ∗ ( z ) \hat f^*(z) f ^ ∗ ( z ) f ^ ( z ) \hat f(z) f ^ ( z )
f ^ ∗ ( z ) = k ^ z x ⊙ α ^ ∗ = k ^ z x ⊙ r e a l ( α ^ ) { {\hat f}^*}(z) = { {\hat k}^{zx} } \odot { {\hat \alpha }^*} = { {\hat k}^{zx} } \odot real(\hat \alpha )
f ^ ∗ ( z ) = k ^ z x ⊙ α ^ ∗ = k ^ z x ⊙ re a l ( α ^ )
其中k ^ z x {\hat k}^{zx} k ^ z x z z z x x x x ^ \hat x x ^