Biot-Savart定律
Biot-Savart定律指出电流元Idl在与其距离为r的空间任意一点P处激发的磁感应强度B的大小为
dB=kr2Idlsinθ
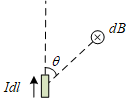
图中dB的方向垂直于屏幕方向向内。公式中的k=4πμ0,μ0是真空磁导率。磁感应强度B的方向满足右手螺旋定则。
载流直导线附近的磁场
计算一根通电长直导线附近一点的磁感应强度B。长直导线是由无数个电流元组成,积分即可。
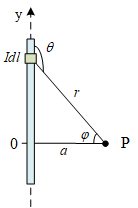
在长直导线上建立坐标轴,与待求位置P水平的位置作为竖直方向的零点。直接积分,积分变量是l,在有了坐标轴的情况下,我们就可以把这个曲线积分转化为定积分。
B=l∫dB=4πμ0Il∫r2sinθdl=4πμ0I∫−∞∞r2sinθdl
但这还是不好求。可以想办法把θ作为积分变量,因为θ是在(0,π)之间变化的。我们需要找到dl与dθ的关系,还有r和θ的关系。
r和θ的关系比较好找:
r=a/cosφ=a/cos(π−θ)=−a/cosθ
l与θ的关系是这样的:
l=atanφ=atan(π−θ)=−atanθ
两边微分后可得:
dl=−adθ/cos2(θ)
再把上面的结果代回到原来的积分式中
B=4πaμ0I∫0πsinθdθ=2πaμ0I
磁偶极矩
在分析问题的时候,除了通电长直导线附近磁场经常用到,还有环形电流轴线上的磁场也经常会遇到。
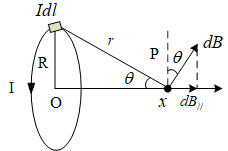
环形电流上每一个电流元到轴线上一点的距离都相等,它们各自产生的磁感应强度叠加后,dB垂直于轴线方向的分量都抵消,只剩平行与轴线方向的分量。
B=l∫dBsinθ=4πr2μ0Isinθl∫dl=4πr2μ0Isinθ⋅2πR=2μ0r2IRsinθ
把sinθ=rR,r=x2+R2代入得:
B=2(x2+R2)3/2μ0IR2
当x趋于无穷大时,x≈r:
B=2πr3μ0IS
S是圆环电流围成的面积。从这个公式中可以看出,圆环电流轴线上远处的某一点(r确定)的B的大小取决于I和S的乘积。因此定义了一个概念——磁偶极矩 pm。
pm=IS
磁偶极矩的方向和磁感应强度的方向相同,满足右手螺旋定则。
磁场的安培环路定理
沿着一个环路对磁感应强度B积分,可以得到一个常量,这个常量由闭合环路内的电流的代数和决定。
L∮Bdl=μ0I
常用安培环路定理计算某些情况下的磁感应强度。比较典型的就是螺绕环内的磁场分布。
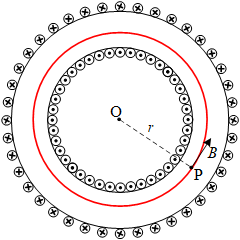
图中螺绕环共N匝,导线电流为I,利用安培环路定理,求P点的磁感应强度B。利用螺绕环内磁场分布的中心对称性,可以对半径为r的环路做积分:
L∮Bdl=B⋅2πr=μ0NI
这样就可以得到:
B=2πrμ0NI=μ0nI
其中n=N/(2πr),表示单位长度的匝数。
当螺绕环无限大时,螺绕环内的磁感应密度处处相等,而螺绕环外的磁感应强度处处为0。这同样可以用安培环路定理,结合磁场分布特点得出这个结论。同时这还可以推广到无限长直螺线管的内外磁场分布情况,因为螺绕环无限大时,其中的每一段都可以看作是无限长直螺线管的一部分。
介质的磁化
某些介质在外磁场的作用下会被磁化,主要分为顺磁质、抗磁质和铁磁质。
顺磁质比较好理解,某种介质,它的分子中的电子激发的磁场可以等效为一个圆环电流。每个分子就是一个磁偶极矩,就像一个小磁铁。在外加磁场的作用下,每个分子都会整整齐齐地排列。
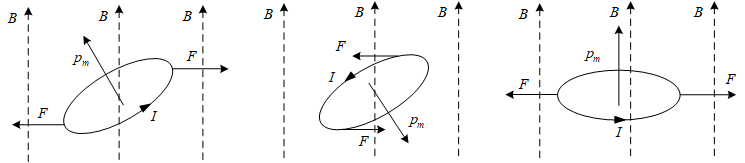
至于为什么会磁化,可以把这里的圆环电流想象成真实的电流圆环,然后用“通电导线在磁场中受到安培力”进行分析。而且这也遵守能量最低原则,当每个磁偶极矩的方向和外加磁场方向一致是,能量最低。
抗磁质需要在更微观的尺度上分析,抗磁质的分子不能等效成电流圆环。但是电子绕原子核旋转时也会有磁偶极矩pm。在施加外加磁场后,这样一个磁偶极矩并不会像前面分子等效的电流圆环那样产生与外磁场同向的磁偶极矩,而是想陀螺一样产生进动。
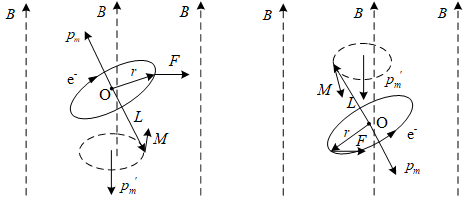
外磁场对电子的洛伦兹力为F,洛伦兹力会产生一个力矩M改变角动量,从而是电子不光沿着电子轨道运动,而且绕着外加磁感线的方向旋转。从而产生额外磁矩pm′,经过分析可以看到额外磁矩pm′的方向始终与外加磁场方向相反,所以对外表现出减弱磁场的效应。这一效应在顺磁质中也有发生,只是这部分减弱的磁场与顺磁质的固有磁矩相比很小。
为了便于分析带磁介质的情况,引入了磁场强度H。在有磁介质的情况下,磁感应强度变为μrB0,μr是介质的相对磁导率。
L∮Bdl=μrL∮B0dl=μrμ0i∑Ii
其中B0表示没有磁介质时的外加磁感应强度。令:
H=μrμ0B
这样带磁介质的安培环路定理就可以表示为:
L∮Hdl=i∑Ii
铁磁质
铁磁质是顺磁质的一种,只是它的相对磁导率μr特别大,而且有磁滞的特性,所以单独拿出来讲。
下图是铁磁质的磁滞回线。
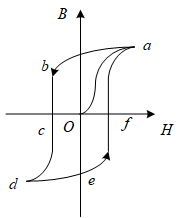
Oa段是起始磁化曲线,随着磁场强度H的增大,磁感应强度并不会一直线性增大,当磁感应强度不再显著变化时,表示达到了磁饱和。
减小磁场强度,如ab段,当H减小为0,磁感应强度也不为0,这个值称为剩磁。只有加反向的磁场,这部分剩磁才会消失。这就像我们让磁介质里的每个分子都统一朝向之后再让它们转向,有时候它们比较迟钝,就需要一个反向的外力才能让它们转向。
实际中我们是会怎样调整磁场强度呢?比如增大线圈中的电流,就能够让H增大。这在变压器、滤波电感等场景中都很常见。一旦发生了磁饱和,表示磁通量的变化跟不上电流的变化,电感感值也不再是标称的感值。轻则信号失真,重则炸板子。
磁滞回线的存在也是产生“铁损”的原因,始终工作在饱和情况下的磁芯会严重发热,越高频越大电流越容易发生饱和。
自感与互感
电路中的电感感值L可能最初是用来描述载流回路与磁通量的关系。
ψ=Li
根据法拉第电磁感应定律,回路中的自感电动势为:
EL=−dtdψ=−Ldtdi
类似自感系数的定义,还可以定义互感系数。定义互感系数M12和M21:
ψ12=M12i2ψ21=M21i1
现有两个匝数相同的线圈,线圈1和线圈2。线圈1的磁通量包含两部分ψ11和ψ12,ψ11是线圈1自感产生的,ψ12是由线圈2互感产生的。同样线圈2也会得到来自线圈1的磁通ψ21。由此可以定义耦合系数K。
K=ψ11ψ21ψ22ψ12
利用能量守恒可以证明M12和M21相等,可以记为M。
K2=ψ11/i1ψ21/i1ψ22/i2ψ12/i2=L1L2M2,K=L1L2M
线圈匝数与线圈的自感系数是平方关系因为每一匝的磁通贡献是Φ=NΦ0,因为每圈电流产生的磁感线通过了N个线圈。所以总磁通为:
ψ=NΦ=N2Φ0
自感系数L=Φ/i=N2L0,L0表示单匝线圈的自感系数。
对于一个全耦合变压器,K=1,M=L1L2,通过计算可以得到下面的等效电路:
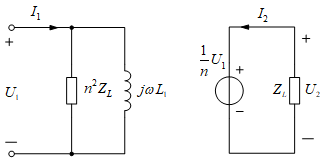
有两个结论:
- 全耦合变压器有阻抗变换的作用,副边的ZL映射到原边为n2ZL
- 副边电压是原边电压的1/n,而与负载无关。