傅里叶变换主要分为连续和离散两大块。对连续时间信号的分析，从周期信号的傅里叶级数展开到统一的傅里叶变换（FS），是一套完整地体系。离散时间信号的傅里叶分析和连续时间信号的分析非常像，但确实是不同，没法统一地表示，主要区别在“求和”和“积分”上。FS，FT，DFS，DTFT，DFT构成了整个傅里叶分析的体系。
  不管是哪种变换，都满足“周期-离散”，“非周期-连续”的对应关系。这个关系对帮助记忆非常有用。

分析方法 缩写 变换过程
时域信号 → 频域信号
傅里叶级数 FS 连续周期 → 非周期离散
傅里叶变换 FT 连续周期 → 非周期离散
连续非周期 → 非周期连续
离散傅里叶级数 DFS 离散周期 → 周期离散
离散时间傅里叶变换 DTFT 离散非周期 → 周期连续
离散傅里叶变换 DFT 离散非周期 → 离散非周期
(本质)离散周期 → 周期离散

连续时间傅里叶分析

傅里叶级数

  连续时间的分析得从傅里叶级数开始讲起。

f(t)=f(t+T0)          f(t)=∑n=−∞+∞ane−jnω0f(t) = f(t + {T_0})\;\;\;\;\;f(t) = \sum\limits_{n = - \infty }^{ + \infty } { {a_n}{e^{ - jn{\omega _0} } } }

  任何周期为T0T_0（频率为f0f_0，角频率为ω0\omega_0）的周期信号，都可以用角频率为ω0\omega_0整数倍的复指数信号e−jnω0e^{ - jn{\omega _0} }线性表示。
  比如余弦信号Acos(ω0t)Acos(\omega_0t)傅里叶级数展开可以表示为：

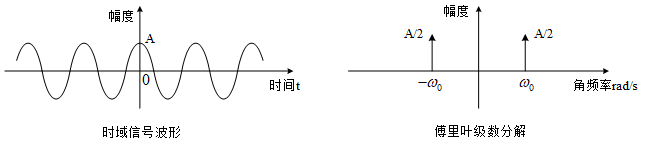
Acos(ω0t)=A2(e−jω0t+ejω0t)Acos(\omega_0t)={A \over 2}\left( { {e^{ - j{\omega_0}t} } + {e^{j{\omega_0}t} } } \right)

  实信号的傅里叶变换得到的幅度谱总是偶对称的，相位谱总是奇对称的。一个余弦信号能分解成两个共轭的复指数信号，如下图所示。

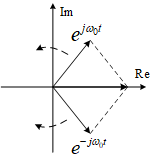
  随着时间tt的增加，它们在复平面上不断转动，但是它们的矢量和总是落在实轴上，对外表现出来就是一个实信号。
  这也是为什么有“负频率”存在的原因，这里的“负”指的是复指数信号的角频率是负数，与“正频率”的信号是共轭关系。相互成共轭关系的复指数信号一同构成实信号。

傅里叶变换

  傅里叶级数仅限于对周期信号的分析，对于非周期信号，可以把信号的周期看作无穷大，基于这样的想法，可以从傅里叶级数的分析合成式推广到傅里叶变换对。

an=1T0∫T0f(t)e−jnω0tdt        f(t)=∑n=−∞+∞anejnω0{a_n} = {1 \over { {T_0} } }\int\limits_{ {T_0} } {f(t){e^{ - jn{\omega _0}t} }dt} \;\;\;\;f(t) = \sum\limits_{n = - \infty }^{ + \infty } { {a_n}{e^{jn{\omega _0} } } }

  ana_n表示傅里叶级数中与基波成nn次谐波关系的复指数信号的系数。把它们写在一起可以得到：

f(t)=∑n=−∞+∞(1T0∫T0f(t)e−jnω0tdt)ejnω0  f(t) = \sum\limits_{n = - \infty }^{ + \infty } {\left( { {1 \over { {T_0} } }\int\limits_{ {T_0} } {f(t){e^{ - jn{\omega _0}t} }dt} } \right){e^{jn{\omega _0} } } } \;

=∫−∞+∞(∫−∞+∞f(t)e−jnω0tdt)ejnω0df= \int_{ - \infty }^{ + \infty } {\left( {\int_{ - \infty }^{ + \infty } {f(t){e^{ - jn{\omega _0}t} }dt} } \right){e^{jn{\omega _0} } }df}

  当T0T_0趋于无穷时，f0f_0趋于无穷小，原来的求和就需要改为积分，微分变量是从原来的1/T01/T_0转变过来的dfdf。

=12π∫−∞+∞(∫−∞+∞f(t)e−jnω0tdt)ejnω0dω= {1 \over {2\pi } }\int_{ - \infty }^{ + \infty } {\left( {\int_{ - \infty }^{ + \infty } {f(t){e^{ - jn{\omega _0}t} }dt} } \right){e^{jn{\omega _0} } }d\omega }

  dfdf到dωd\omega需要乘以2π2\pi，所以最后傅里叶变换的合成式里就有一个1/2π1/2\pi的系数。

X(jω)=∫−∞+∞f(t)e−jωtdt            f(t)=12π∫−∞+∞X(jω)ejωtdωX(j\omega ) = \int_{ - \infty }^{ + \infty } {f(t){e^{ - j\omega t} }dt} \;\;\;\;\;\;f(t) = {1 \over {2\pi } }\int_{ - \infty }^{ + \infty } {X(j\omega ){e^{j\omega t} }d\omega }

周期与非周期信号的统一

  在引入了冲激信号δ(t)\delta(t)之后，周期信号和非周期信号的傅里叶变换得到了统一。因为傅里叶变换的分析式是在无穷范围内的积分，周期信号做这样的积分无法收敛。
  周期信号可以分解成多个复指数信号之和。所以我们只要能表示出复指数信号的傅里叶变换就可以得到周期信号的傅里叶变换。再结合傅里叶变换的频移性质：

ejω0tx(t)⇔X(j(ω−ω0)){e^{j{\omega _0}t} }x(t) \Leftrightarrow X\left( {j\left( {\omega - {\omega _0} } \right)} \right)

  我们只要知道"1"的傅里叶变换就能得到复指数信号的傅里叶变换。具体的求解过程有人写过，文章中给出了比较完整的推导过程，这里就不详细说了，结果是下面这个：

1⇔2πδ(ω)1 \Leftrightarrow 2\pi \delta \left( \omega \right)

  这个结果也很自然成立，把2πδ(ω)2\pi \delta \left( \omega \right)代入到傅里叶变换合成式里很明显就能成立。

F(Acos⁡(ω0t))=A2⋅2πδ(ω−ω0)+A2⋅2πδ(ω+ω0){\cal F}\left( {A\cos ({\omega _0}t)} \right) = {A \over 2} \cdot 2\pi \delta \left( {\omega - {\omega _0} } \right) + {A \over 2} \cdot 2\pi \delta \left( {\omega + {\omega _0} } \right)

  所以周期信号的傅里叶变换的结果会包含2πδ(ω−ω′)2\pi \delta \left( {\omega - {\omega'} } \right)的冲激信号，而且每个冲激信号前面的系数正好是对应的傅里叶级数的各个系数。

离散时间傅里叶变换

  离散时间的傅里叶变换和连续时间的傅里叶变换有很多相似的地方，但它们俩又是两套完全不同的分析体系，最大的区别在于从“积分”变为了“求和”。

离散傅里叶级数

  傅里叶变换的本质是在频域对信号进行正交分解。在连续时间信号的情况下，对一个频率为ω0\omega_0的周期信号来说，就是将它投影到ω0\omega_0、2ω02\omega_0、3ω03\omega_0等这些与基频成谐波关系的频率上去。
  连续的情况下，谐波是无限的.而在离散的情况下，周期为NN的数字序列，基频可以表示为2π/N2\pi/N，由于复指数信号的周期性：

e−j2π/N=e−j2π(N+1)/N{e^{ - j2\pi /N} } = {e^{ - j2\pi (N + 1)/N} }

  所以在离散的情况下，一个周期为N的序列，只能在频域上分解为N个不同的复指数序列。

X~[k]=∑n=0N−1x~[n]WNkn        x~[n]=1N∑n=0N−1X~[k]WN−kn\widetilde X[k] = \sum\limits_{n = 0}^{N - 1} {\widetilde x[n]W_N^{kn} } \;\;\;\;\widetilde x[n] = {1 \over N}\sum\limits_{n = 0}^{N - 1} {\widetilde X[k]W_N^{ - kn} }

  上面是离散傅里叶级数的分析式和合成式，WNknW_N^{kn}是对e−j2πknNe^{-j2\pi\frac{kn}{N} }的简记，也叫做旋转因子。
  离散傅里叶级数，不管是时域的数字序列还是频域的复指数序列都是周期的x~[n]\widetilde x[n]和X~[n]\widetilde X[n]上的波浪线表示它们是周期信号。

离散傅里叶变换

  先直接给出离散傅里叶变换的分析式和合成式：

X[k]=∑n=0N−1x[n]WNkn,    0≤k≤N−1X[k] = \sum\limits_{n = 0}^{N - 1} {x[n]W_N^{kn} } ,\;\;0 \le k \le N - 1

x[n]=1N∑n=0N−1X[k]WN−kn,    0≤n≤N−1x[n] = {1 \over N}\sum\limits_{n = 0}^{N - 1} {X[k]W_N^{ - kn} } ,\;\;0 \le n \le N - 1

  离散傅里叶变换也是为了处理非周期序列的分析问题，这里干脆就直接把非周期序列看作是周期序列，相当于从离散傅里叶级数中截取一个周期长度的序列来表示。这就是DFT固有的周期性。

离散时间傅里叶变换

  课本上在讲DFT之前还讲了DTFT，这是正统的分析有限长序列的频谱的方法。它也是通过离散傅里叶级数，令N趋于无穷得到的。下面是DTFT的分析式和合成式：

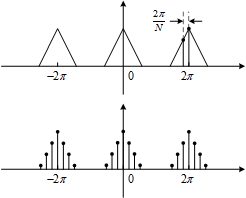
x[n]=12π∫2πX(ejω)ejωndω        X(ejω)=∑n=−∞+∞x[n]e−jωnx[n] = {1 \over {2\pi } }\int\limits_{2\pi } {X\left( { {e^{j\omega } } } \right){e^{j\omega n} }d\omega } \;\;\;\;X\left( { {e^{j\omega } } } \right) = \sum\nolimits_{n = - \infty }^{ + \infty } {x[n]{e^{ - j\omega n} } }

  DTFT得到的频谱是周期连续的频谱，并且是以2π2\pi为周期，就像下面这样：

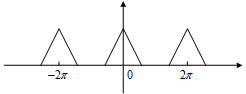
  如果将这个有限长序列按照它的长度NN进行周期延拓，相当于将它和一个周期为NN的冲激串（由单位冲激函数组成的序列）卷积。时域卷积相当于频域相乘。时域周期为NN的冲激串在频域就是周期为2π/N2\pi/N的冲激串。所以有限长序列的DFT相当于在其DTFT的频谱上采样。