本文是关于最小二乘问题的一些总结。

问题引入

  最小二乘法最常见于曲线拟合的问题。比如有一组样本点(x1,y1)(x_1, y_1), (x2,y2)(x_2, y_2), (x3,y3)(x_3, y_3), …, (xm,ym)(x_m, y_m)。每个样本点的xx都是n-1维列向量。然后根据用户定义的模型可以列出m个方程组成的方程组来求解模型中的参数。
  以x∈C3x \in { {\rm{C} }^3}为例，每个样本是3维的数据，共5组样本数据，列出一次多项式方程组，求解n个参数a,b,c,da, b, c, d：

{ax11+bx12+cx13+d=y1ax21+bx22+cx23+d=y2ax31+bx32+cx33+d=y3ax41+bx42+cx43+d=y4ax51+bx52+cx53+d=y5\left\{ \begin{array}{l} ax_{11} + bx_{12} + c{x_{13} } + d = {y_1}\\ ax_{21} + bx_{22} + c{x_{23} } + d = {y_2}\\ ax_{31} + bx_{32} + c{x_{33} } + d = {y_3}\\ ax_{41} + bx_{42} + c{x_{43} } + d = {y_4}\\ ax_{51} + bx_{52} + c{x_{53} } + d = {y_5} \end{array} \right.

  也可以采用更加复杂的模型，例如：

{aex11+bx12+cln⁡x13+d=y1aex21+bx22+cln⁡x23+d=y2aex31+bx32+cln⁡x33+d=y3aex41+bx42+cln⁡x43+d=y4aex51+bx52+cln⁡x53+d=y5\left\{ \begin{array}{l} a{e^{ {x_{11} } } } + \frac{b}{ { {x_{12} } } } + c\ln {x_{13} } + d = {y_1}\\ a{e^{ {x_{21} } } } + \frac{b}{ { {x_{22} } } } + c\ln {x_{23} } + d = {y_2}\\ a{e^{ {x_{31} } } } + \frac{b}{ { {x_{32} } } } + c\ln {x_{33} } + d = {y_3}\\ a{e^{ {x_{41} } } } + \frac{b}{ { {x_{42} } } } + c\ln {x_{43} } + d = {y_4}\\ a{e^{ {x_{51} } } } + \frac{b}{ { {x_{52} } } } + c\ln {x_{53} } + d = {y_5} \end{array} \right.

  求解的时候所有的样本点都是会代入方程组中的，所以只要待求的参数最后能组成线性的方程组就行。
  在线性代数中我们学过线性方程组解的结构。

[x11x12x131x21x22x231x31x32x331x41x42x431x51x52x531][abcd]=A[abcd]=[y1y2y3y4] {\begin{bmatrix} {x_{11} }&{x_{12} }&{ {x_{13} } }&1\\ {x_{21} }&{x_{22} }&{ {x_{23} } }&1\\ {x_{31} }&{x_{32} }&{ {x_{33} } }&1\\ {x_{41} }&{x_{42} }&{ {x_{43} } }&1\\ {x_{51} }&{x_{52} }&{ {x_{53} } }&1 \end{bmatrix} } {\begin{bmatrix} a\\ b\\ c\\ d \end{bmatrix} } = A {\begin{bmatrix} a\\ b\\ c\\ d \end{bmatrix} } = {\begin{bmatrix} { {y_1} }\\ { {y_2} }\\ { {y_3} }\\ { {y_4} } \end{bmatrix} }

  可以把前面的第一个方程组写成矩阵的形式，系数用矩阵A表示，A的秩rank(A)\rm rank(A)如果小于n（n是参数的个数），那么就有无穷解；rank(A)=n\rm rank(A)=n，则有唯一解；rank(A)>n\rm rank(A)>n则无解。这和我们熟知的，要解n个变量，就需要n个方程是一个道理。
  最小二乘法主要用在“无解”的情况，在实际应用中，采集大量样本数据后，往往是得不到唯一解的。但我们想要得到一个曲线能最好地描述这一批数据，最小二乘法就是能得到令估计误差的平方和最小的一种估计方法。
  而最佳体现在哪里？一般很少会有人提到最佳的最小二乘解是因为在“无解”的情况下，最小二乘解是唯一的，而只有在“无穷解”的情况下才有“最佳”的说法。而在“无穷解”的情况下相当于是在用极少的样本估计模型的参数，这在实际应用中一般也是没有意义的，所以“最佳”这个概念基本没人提。

问题的数学描述

  目标函数可以这样表示：

arg⁡min⁡ω∥Xω−Y∥22\mathop {\arg \min }\limits_\omega {\left\| {X\omega - Y} \right\|_2^2}

  ω\omega是一个n维的列向量，是我们需要估计的参数。XX是一个m×nm\times n的矩阵，每一行对应一个样本数据，共m行，也就是说有m个方程；YY是每个样本的标签值组成的m×1m\times 1的列向量。
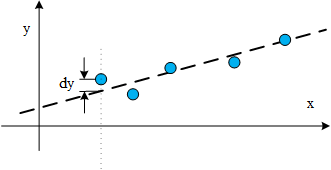
  几何意义就是样本点与估计的曲线的偏差dydy越小越好，目标函数取的是误差向量的二范数，忽略了偏差的正负。

解析推导

  我之前在关于CSK与KCF算法推导（二）中写了岭回归的推导，岭回归就是在最小二乘的基础上加上了正则项，保证了ω\omega一定有解。这里的推导和岭回归几乎一致。
  类似二次多项式求最小值的问题，目标函数对ω\omega求偏导，令其偏导为零向量即可求出ω\omega在什么情况下能令目标函数最小化。

∂∥Xω−Y∥22∂ω=0\frac{ {\partial \left\| {X\omega - Y} \right\|_2^2} }{ {\partial \omega } } = 0

  将目标函数展开，向量二范数的平方就是向量内积：

∥Xω−Y∥22=(Xω−Y)T(Xω−Y)=ωTXTXω−ωTXTY−YTXω+YTY\left\| {X\omega - Y} \right\|_2^2 = {\left( {X\omega - Y} \right)^T}\left( {X\omega - Y} \right) = {\omega ^T}{X^T}X\omega - {\omega ^T}{X^T}Y - {Y^T}X\omega + {Y^T}Y

  每一项分别对ω\omega求偏导：

∂ωTXTXω∂ω=XTXω+(ωTXTX)T=2XTXω\frac{ {\partial {\omega ^T}{X^T}X\omega } }{ {\partial \omega } } = {X^T}X\omega + {\left( { {\omega ^T}{X^T}X} \right)^T} = 2{X^T}X\omega

∂ωTXTY∂ω=XTY\frac{ {\partial {\omega ^T}{X^T}Y} }{ {\partial \omega } } = {X^T}Y

∂YTXω∂ω=(YTX)=XTY\frac{ {\partial {Y^T}X\omega } }{ {\partial \omega } } = \left( { {Y^T}X} \right) = {X^T}Y

∂YTY∂ω=0\frac{ {\partial {Y^T}Y} }{ {\partial \omega } } = 0

  整合起来令偏导为零向量：

2(XTXω−XTY)=02\left( { {X^T}X\omega - {X^T}Y} \right) = 0

  也就是：

XTXω=XTY{X^T}X\omega = {X^T}Y

  如果没有额外的条件的话是无法保证XTXX^TX可逆的，如果XTXX^TX可逆，那么：

ω=(XTX)−1XTY\omega = {\left( { {X^T}X} \right)^{ - 1} }{X^T}Y

  XTXX^TX可逆也不难，只要XX是列满秩的就行。XX是m×nm\times n的矩阵，一般情况下样本个数m远大与待求的变量个数n时，XX列满秩是很容易满足的。

从正交投影矩阵的角度推导

  参考了华中科技大学出版社的《矩阵论》（第二版）教材，书中关于最佳的最小二乘解的内容得从M-P广义逆开始说起。求最佳的最小二乘解是M-P广义逆的一个应用，想要详细了解的小伙伴建议直接看书，我这里写的东西难免有些不严谨的地方，而且没法真正地把这个思路讲明白。书中的结论是更加一般化的，前面的推导的结果是其中的一个特例。

M-P广义逆

  书中介绍了M-P广义逆的一些性质，这里就不写了，主要提一下怎么计算M-P广义逆。任意矩阵A∈Cm×nA \in { {\rm{C} }^{m \times n} }都存在M-P广义逆A+A^+。先对AA进行满秩分解，

A=BC,  B∈Cm×r,  C∈Cr×n,  rank(B)=rank(C)=rA = BC,\;B \in { {\rm{C} }^{m \times r} },\;C \in { {\rm{C} }^{r \times n} },\;{\mathop{\rm rank}\nolimits} (B) = {\mathop{\rm rank}\nolimits} (C) = r

M-P广义逆就可以表示为，

A+=CH(CCH)−1(BHB)−1BH{A^ + } = {C^H}{\left( {C{C^H} } \right)^{ - 1} }{\left( { {B^H}B} \right)^{ - 1} }{B^H}

特别的，当AA为列满秩的矩阵时，C=Ir×rC=I_{r\times r}，

A+=(AHA)−1AH{A^ + } = {\left( { {A^H}A} \right)^{ - 1} }{A^H}

正交投影矩阵

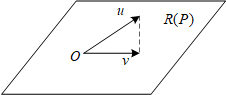
  正交投影矩阵PP满足：P2=P,  PH=PP^2=P,\;P^H=P。正交投影矩阵有什么用呢？假如P∈Cn×nP \in { {\rm{C} }^{n \times n} }，是一个正交投影矩阵，

v=Pu,u∈Cn×1,v∈Cn×1v=Pu, u \in \rm C^{n\times 1}, v \in \rm C^{n\times 1}

uu经过PP变换以后可以得到一个R(P)R(P)空间中的一个向量vv,

∥v−u∥2≤∥x−u∥2,  ∀x∈R(P){\left\| {v - u} \right\|_2} \le \left\| {x - u} \right\|_2,\;\forall x \in R(P)

向量vv与uu之间的欧式距离小于R(P)R(P)空间中的任何向量xx

  考察矩阵AA+AA^+和矩阵A+AA^+A可以发现它们都是正交投影矩阵。书中有证明R(AA+)=R(A)R(AA^+)=R(A)，这为我们带来了很大的方便。如果我们想把向量xx正交投影到R(A)R(A)空间，只需要计算AA+xAA^+x就行了。

回到问题

arg⁡min⁡ω∥Xω−Y∥22\mathop {\arg \min }\limits_\omega {\left\| {X\omega - Y} \right\|_2^2}

  再回到原来的问题，我们想找的就是XωX\omega如果能是YY在R(X)R(X)空间中的正交投影就好了，前面的结论就告诉了我们XX+YXX^+Y就是YY在R(X)R(X)空间中的正交投影。那么自然，

ω=X+Y\omega = {X^ + }Y

  与前面的解析推导不一样的地方是，这里没有对XX的形式做限制。如果同样加上XX是列满秩的限制，那么可以得到与前面一样的结论。

ω=(XTX)−1XTY\omega = {\left( { {X^T}X} \right)^{ - 1} }{X^T}Y

  ω=X+Y\omega = {X^ + }Y是一个更加一般的结论，它被称为“最佳的最小二乘解”。这个解不光满足最小二乘，而且这个解本身的二范数也是最小的，所以是所有最小二乘解中最佳的解。而“最佳”也只会在有无穷解的情况下体现，下面举个最简单的例子。

举例

  用样本点(1,2)拟合一条直线，y=ax+by=ax+b。

[11][ab]=2{\begin{bmatrix} 1&1 \end{bmatrix} } {\begin{bmatrix} a\\ b \end{bmatrix} } = 2

X=[11],  X+=XT(XXT)−1=[0.50.5]X = {\begin{bmatrix} 1&1 \end{bmatrix} },\;{X^ + } = {X^T}{\left( {X{X^T} } \right)^{ - 1} } = {\begin{bmatrix} {0.5}\\ {0.5} \end{bmatrix} }

最佳的最小二乘解：

[ab]=X+Y=[11] {\begin{bmatrix} a\\ b \end{bmatrix} } = {X^ + }Y = {\begin{bmatrix} 1\\ 1 \end{bmatrix} }

  过点(1,2)的直线有无数条，这无数条直线的参数a,ba,b都是这一问题的最小二乘解，它们都能令Xω−Y=0X\omega-Y=0，而这些解中a=1,b=1a=1,b=1是最佳的，因为此时a2+b2a^2+b^2最小。